Calculation of Right Ascension and Declination

Main artile: https://paulplusx.wordpress.com/2016/03/02/rtpts_azalt/

The Idea!- Kepler’s Algorithms

Yes! The real-time position of any celestial body can be calculated using some parameters called Orbital Elements (or Osculating Elements or Keplerian Elements). These are the parameters that define an orbit at a particular time.

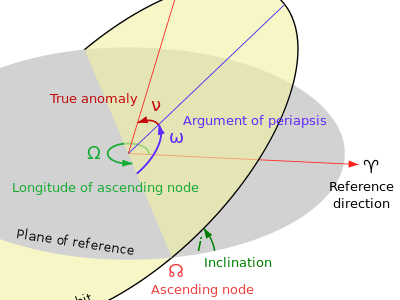
• Inclination (i) - angle between the plane of the Ecliptic and the I. In this diagram the orbital plane (yellow) intersects a reference plane. For Earth-orbiting satellites, the reference plane is usually the earths equatorial plane and for satellites in the solar orbits it is the elliptic plane. The intersection is called e plane of the orbit.

• Longitude of the Ascending Node (o) - states the position in the orbit where the elliptical path of the planet passes through the plane of the ecliptic, from below the plane to above the plane.

• Longitude of Perihelion (p) - states the position in the orbit where the planet is closest to the Sun.

• Mean distance (a) - the value of the semi-major axis of the orbit – measured in Astronomical Units for the major planets.

• Daily motion (n) - states how far in degrees the planet moves in one (mean solar) day. This figure can be used to find the mean anomaly of the planet for a given number of days either side of the date of the elements. The figures quoted in the Astronomical Almanac do not tally with the period of the planet as calculated by applying Kepler’s 3rd Law to the semi-major axis.

• Eccentricity (e) - eccentricity of the ellipse which describes the orbit.

• Mean Longitude (L) - Position of the planet in the orbit on the date of the elements (Source:2).

All the above parameters are change constantly (but very very slowly) due to gravitational perturbations by other objects and the effects of relativity because of that we need to take the latest orbital elements into our calculation for least possible error or highest accuracy. I just googled and got orbital elements for the year 2013 (text). You can try different methods or go to the following sites to gather data.

• http://asa.usno.navy.mil/SecE/Osculating_Elements.html

• http://ssd.jpl.nasa.gov/ 

• http://www.imcce.fr/langues/en/

• http://naif.jpl.nasa.gov/naif/

• Research gate forum

Now that you have the latest osculating (orbital) elements for a date lets say 16 August 2013, we will start our calculations but before that we need to know few terms.

• JDN – An Integer (Julian Day No.) that would give the day number count from the beginning of Julian year which will help us locating the planets/celestial bodies in their orbits for a particular date and time relative to a particular date.

• Equatorial Coordinate System – The coordinates Right Ascension (RA) and Declination (DEC) will be used frequently here.Look at the GIF  to know what is RA and DEC.

The positions of objects in the sky as viewed from Earth are referred to a coordinate system whose alignment is changing with time in a complex way. A few of the important motions and effects are summarized below;

• The Earth is rotating on its axis once every siderial day

• The rotation axis is moving in a circle with a period of roughly 26,000 years (precession)

• The axis is ‘nodding’ up and down with a period of roughly 19 years (nutation)

• The finite speed of light (sometimes referred to as ‘aberration’ in some books)

The ‘fixed’ stars provide a reference system which allows us to account for the daily rotation of the Earth on its axis. We use the Equatorial coordinate system to refer positions to a frame in which the stars appear still, and the right ascension (RA) and declination (DEC) are used to give the coordinates of the planet with respect to the fixed stars. The ‘zero’ of RA is referred to the ‘vernal equinox’, in the same way that the ‘zero’ of longitude is taken as the Greenwich Meridian.

The precession of the equinoxes means that the ‘zero’ of RA is changing slowly with time, which means that star coordinates must always be referred to an epoch, or date. By using orbital elements referred to the fundamental epoch J2000, the orbits of the planets are described in a coordinate system which is based on the position the vernal equinox will have at J2000. A further advantage of this dodge is that our positions for the planets will correspond exactly to the positions found in most recent star charts. You should be able to plot the path of Mars directly onto a star chart such as The Cambridge Star Atlas.

Nutation (which is a small effect anyway) can also be spirited away by referring our positions to the ‘mean ecliptic of J2000’. The word ‘mean’ indicates that no allowance for nutation has been made. Our observation platform (the Earth) is nodding, so the stars and planets will appear to nod together. Our J2000 elements will give is positions which match the co-ordinates of the stars found in star maps.

There is a problem with this use of J2000 equinox and mean ecliptic. If I just dial the values for RA and DEC into a computerized telescope, then the planet will not appear in the center of the field of view – as the RA and DEC will not be referred to the ‘equinox and true ecliptic of date’. The effect will be very small for 10 years either side of J2000 (source:2).

So we would increase the accuracy by using elements from 2013.

Orbital Elements for 16th August 2013

JD = 2450680.5
Equinox and mean ecliptic of J2000.0
       Earth          Mars
i     0.0       1.8496   
o     0.0       49.668
p     103.147   336.322
a     1.0000    1.523762
n     0.985611  0.523998
e     0.016679  0.093346
L     324.5489  82.9625
The values for the other planets can be found in
the C program below.

Calculation

The sections below deal with calculating the RA and DEC of a planet from the osculating elements. Lets find the position of Mars at UT on the 1st of March 2016. The main steps in the calculation are:

• Finding the position of the planet in its orbit

• Find the number of days since the date of the elements

• Find the mean anomaly from the Mean Longitude and the daily motion

• Find the true anomaly using the Equation of Centre

• Find the radius vector of the planet

• Refer that position to the Ecliptic – hence find the heliocentric ecliptic coordinates of the planet

• Repeat most of above to find the heliocentric coordinates of the Earth

• Transform the heliocentric coordinates to geocentric coordinates by a change of origin

• Transform the geocentric ecliptic coordinates to geocentric equatorial coordinates by a rotation about the X axis

• Calculate the RA and DEC and Earth – planet distance from the rectangular coordinates

The method used here was adapted from Paul Schlyter’s page ‘How to compute planetary positions’ at source:3.

Notation

Elements
i - inclination
o - longitude of ascending node at date of elements 
p - longitude of perihelion at date of elements 
a - mean distance (au)
n - daily motion 
e - eccentricity of orbit
l - mean longitude at date of elements
Calculated quantities
M - mean anomaly (degrees)
V - True anomaly (degrees)
r - radius vector (au) referred to current coordinate origin
X - recangular coordinate (au)
Y - recangular coordinate (au)
Z - recangular coordinate (au)
alpha - right ascension (hours or decimal degrees according to
context)
delta - declination (decimal degrees)

Position of the planet in its orbit.

Number of days from date of elements (d).

What you need:

• ‘day number’ (dele) of the elements

• ‘day number’ you want the position for (dpos)

d = dpos - dele

The ‘day number’ can be the

• Julian day, or

• The number of days since the fundamental epoch J2000. I use the second alternative as less precision is needed for the numbers!

The following tables show the days from the beginning of the year to the beginning of each month, and the days from J2000 to the beginning of each year.

Days to beginning of month
        Month   Normal year    Leap year
        Jan         0             0
        Feb        31            31
        Mar        59            60
        Apr        90            91
        May       120           121
        Jun       151           152
        Jul       181           182
        Aug       212           213
        Sep       243           244
        Oct       273           274
        Nov       304           305
        Dec       334           335
        Days since J2000 to beginning of each year
                  Days
        1999     -366.5
        2000       -1.5
        2001      364.5
        2002      729.5
        2003     1094.5
        2004     1459.5
        2005     1825.5
Similarly,
        2013     4747.5
        2016     5842.5

We can find the day number corresponding to the date of the elements (16th August 2013) as follows:

dele = 212 + 16 + 4747.5 = 4975.5

And the day number of the date we want the position for (1st Aprih 2016) is:

dpos = 60 + 1 + 5842.5 = 5903.5

So the number of days after the date of the elements is:

dpos  -  dele  =  d
        5903.5- 4975.5 = 928 days

i.e. 928 days after the elements. You must take dates before an epoch as negative in the calculations below.

For fast moving planets such as Mercury and Mars, you need to include the time of day which you want the position for. Just add the Universal Time in decimal hours divided by 24 to the day number of your position (dele above):

day fraction = (H + M/60)/24 
    
      H is hours UT
      M is minutes UT

Finding the Mean Anomaly of the planet

The Mean Anomaly of the planet is given by the very simple formula:

M = n * d + L - p 
        n is daily motion
        d is the number of days since the date of the elements
        L is the mean longitude
        p is the longitude of perihelion 
        M should be in range 0 to 360 degrees, add or subtract
          multiples of 360 to bring M into this range.

For our case of Mars and 928 days since the date of the elements:

n = 0.523998
        d = 928
        L = 82.9625
        p = 336.322
        M = 0.523998 * 928 + 82.9625 - 336.322
          = 232.910644

Finding the true anomaly of the planet

Mean Anomaly is calculated considering the orbit to be circular, but True Anomaly gives the actual position of the planet as it considers orbit to be elliptical. We convert Mean Anomaly to True Anomaly using the following formula:

v = M + 180/pi * [ (2 * e - e^3/4) * sin(M) + 5/4 * e^2 * sin(2*M)
                             + 13/12 * e^3 * sin(3*M)........ n terms ]
         v is true anomaly
         M is mean anomaly
         e is eccentricity
         pi is 3.14159...
         e^3 means the third power of e. Note how the third
         power is involved the first term as well as the last.
A more expanded series can give a better result so this is what i have used 
in my code :
 v = m + (2 * e - 0.25 *pow(e,3) + 5/96 * pow(e,5)) * sin(m) +
 (1.25 * pow(e,2) - 11/24 * pow(e,4)) * sin(2*m) + 
(13/12 * pow(e,3) - 43/64 * pow(e,5)) * sin(3*m) + 
103/96 * pow(e,4) * sin(4*m) + 1097/960 * pow(e,5) * sin(5*m);

This is manually  calculated using the Equation of Center from “The Astronomical Almanac (page E4)”. For our Mars position, we have:

M = 232.910644 degrees or 4.065057601 radians
    e = 0.093346
Therefore,
    v = 224.9688989 degrees  or 3.926448  radians
Note: In my code I have done all the calculations in  Radians

Finding the radius vector of the planet

The distance from the planet to the focus of the ellipse is given by a simple formula based on the geometry of the ellipse:

r = a * (1 - e^2) / [1 + e * cos(v)]
  
          a is the semi-major axis
          e is the eccentricity
          v is the true anomaly
          the radius vector r will be in the same units as a
          a.u. in this case.

In our Mars calculation we have:

a = 1.523762
e = 0.093346
v =224.9688989
r = 1.523762 * (1 - 0.093346^2) / [ 1 + 0.093346 * cos (224.9688989) ]
  = 1.617293 a.u

Heliocentric coordinates of the planet

Having found the true anomaly and the radius vector of the planet, we can go on to find the position of the planet with respect to the plane of the ecliptic. The formulas below are a combination of ‘resolving’ to find components and rotations around various axes to transform the coordinates to the Ecliptic frame. We might expect the formulas to involve the inclination of the planet’s orbit (i), and various angles within the plane of the orbit, as well as the longitude of the ascending node (o).

X = r * [cos(o) * cos(v + p - o) - sin(o) * sin(v + p - o) *
    cos(i)]
    Y = r * [sin(o) * cos(v + p - o) + cos(o) * sin(v + p - o) *
    cos(i)]
    Z = r * [sin(v + p - o) * sin(i)]
    r is radius vector
    v is true anomaly
    o is longitude of ascending node
    p is longitude of perihelion
    i is inclination of plane of orbit
    the quantity v + p - o is the angle of the planet measured
    in the plane of the orbit from the ascending node

In the case of Mars we have:

r = 1.617293
    v = 224.9688989
    o = 49.668
    p = 336.322
    i = 1.8496
    v + p - o = 511.6228989 - 360 = 151.6228989
    and I get the following rectangular coordinates;
    X  = -1.506606
    Y  = -0.587503
    Z  =  0.024809
    SQRT(X^2 + Y^2 + Z^2) should be same as r

Heliocentric coordinates of Earth

Similarly find M(mean anomaly), V(true anomaly) and r(radius vector) for Earth. We simplify the equations for Earth, as the inclination of the Earth’s orbit is very small. So:

Xe = r * cos(v + p)
   Ye = r * sin(v + p)
   Ze = 0
   r is radius vector of Earth
   v is true anomaly for Earth
   p is longitude of perihelion for Earth

For the problem in hand we have:

after calculations we have
   Xe  = -0.935762
   Ye  =  0.325870
   Ze  =  0.000000

Geocentric ecliptic coordinates of the planet

Just subtract  Earth’s coordinates from those of the planet and we get geocentric (earth as a center ) coordinates.

X' = X - Xe
   Y' = Y - Ye
   Z' = Z - Ze

We then have the geocentric ecliptic coordinates of the planet. For the case of Mars (1st March 2016) we have:

X' = -0.570844
   Y' = -0.913374
   Z' =  0.024809

Geocentric equatorial coordinates of the planet

To change the coordinate system from geocentric ecliptic to geocentric equatorial is just a matter of a rotation around the X axis by an angle equal to the ‘obliquity of the Ecliptic. The X axis points towards the ‘First point of Aries’, which is the direction in space associated with the equinox. As we are using elements referred to the equinox of J2000.0, we use the obliquity for that epoch, which is 23.439292 degrees. The formulas are given below:

Xq = X'
    Yq = Y' * cos(ec) - Z' * sin(ec)
    Zq = Y' * sin(ec) + Z' * cos(ec)
    Xq are the equatorial coordinates
    X' are the geocentric ecliptic coordinates      
    ec is the obliquity of the ecliptic

For Mars, we have:

Xq = -0.570844
    Yq = -0.847872
    Zq = -0.340557

Rectangular coordinates are not much use with star charts, so we calculate the familiar right ascension and declination using the formulas:

alpha = arctan(Yq/Xq)
     
    If Xq is negative then add 180 degrees to alpha  
    If Xq is positive and Yq is negative then add 360 degrees to
    alpha
    alpha is usually expressed in hours, so divide by 15
    delta = arctan( Zq / SQRT(Xq^2 + Yq^2)) 
    distance = SQRT( Xq^2 + Yq^2 + Zq^2)

For Mars on the 1stMarch 2016 we have:

(right ascension) alpha = 15.440000 hrs
          
  (declination)  delta = -18.250000 degs
         
   distance = 1.077971278 a.u.

With this, one of the hardest parts of our project is done!😀

Azimuth and Elevation (Altitude) conversion from RA and DEC [equitorial coordinates to horizontal coordinates]

Now that we have RA and DEC it gives us the value from the vernal equinox at 1st March 2016, therefore we need to give our position in order to see with respect to us (the observer as center ). So we first take the latitude(lat) and longitude(long) using a GPS module of our current location.

For those who are wondering what is Azimuth and Elevation have a look of this image

Note: We will be connecting a GPS module to our Arduino setup to constantly refresh and update our coordinates. Now lets proceed with the calculation.

We need to know:

• Local Sidereal Time– First we need the time (hour and minute in UT) and the day no of the date 1st march 2016 [i.e. dpos= 5903.5 ] . Now we use this formula to get LST.

LST = (100.46 + 0.985647 * day + Long + 15 * (hour + minute / 60) + 360) – (((int)                ((100.46 + 0.985647 * day + Long + 15 * (hour + minute / 60) + 360)/360))*360);

• Hour Angle

HA = (LST – RA + 360)- ((int)((LST – RA + 360)/360))*360 ;

• HA, DEC, Lat to Alt, AZ

x = cos(HA * (pi / 180)) * cos(Dec * (pi / 180)); y = sin(HA * (pi / 180)) *cos(Dec * (pi / 180)); z = sin(Dec * (pi / 180));

• Horizontal coordinates:

xhor = x * cos((90 – Lat) * (pi / 180)) – z *sin((90 – Lat) * (pi / 180)); yhor = y; zhor = x * sin((90 – Lat) * (pi / 180)) + z *cos((90 – Lat) * (pi / 180));
az = atan2(yhor, xhor) * (180 / pi) + 180;  alt = asin(zhor) * (180 / pi);

If you want to know more about these formulae  then do some research. So finally we have the result as:

Azimuth = 193.845997 degrees
Altitude = 58.017963 degrees

This is my Repo link: Github.

We can feed these values to our pan-tilt servo mechanism with proper mapping. References:

• http://www.stargazing.net/kepler/ellipse.html

• http://www.stjarnhimlen.se/comp/tutorial.html