Existing blockchain Proof-of-Work (PoW) algorithms have contributed to the scarcity of certain types of compute resources (e.g. GPUs) and are responsible for intense energy consumption, resulting in a large amount of carbon emissions. Depending on the blockchain or cryptocurrency in question, they also tend to be inaccessible to small players without access to the latest ASICs or inexpensive power.
In order to address this problem, I have attempted to design and implement a novel class of PoW algorithm: Proof of Configurability (PoC), a class of PoW algorithm that is best suited for execution on FPGAs. I have dubbed my particular algorithm "Tleilax, " a nod to a group of people in a certain science fiction series that are able to shape-shift their faces.
Traditional PoW relies on raw compute power, and accordingly is best suited for execution on purpose-built ASICs. Other classes of “ASIC-resistant” PoW algorithms exist, and thus rely on different computing resources for scarcity: “Proof of I/O” (e.g. ethash) relies on high memory bandwidth, making it best suited for execution on GPUs, and “Proof of Space” relies not on compute but on storage capacity, requiring large amounts of storage media. Tleilax differs from these existing ASIC-resistant solutions in that it relies on capacity for reconfigurable computing. It is therefore useful in that it provides more options for PoW implementation to the decentralized computing community and leverages a class of compute resource that is currently underutilized in the space: FPGAs.
Card installation and coolingI installed my Varium C1100 in a PCIe slot of my Ubuntu 20.04 workstation. I ran the Xilinx Ethereum mining demo, as well as Ethereum mining with Team Red Miner, and quickly realized the airflow provided by my case fans was insufficient. First, I attempted to jerry-rig a cardboard cooling shroud that redirected airflow from the intake fan in the bottom of my case to the card, which you can see below.
This helped marginally, but was insufficient. I happened to find an old blower fan in my local electronics store and decided to give it a shot. In the gallery of pictures below, you can see how I modified the blower to fit around the auxiliary power connector and attached it non-destructively with zip ties. Ultimately this proved successful, as with the blower I am able to run workloads for extended periods of time while remaining at reasonable temperatures.
The Tleilax algorithm is based on an N x N reconfigurable architecture of hashing, where multiple layers of hashing units are connected in ever-changing patterns in order to produce a final hash. The number of layers and size of each layer, N, is determined according to the following equation:
N = (previous_nonce % M) + C
Where C is a constant offset, to avoid the hashing architecture randomly becoming zero or too small. Implementations of Tleilax can specify M and C to their liking, and are referred to as Tleilax-M+C. For instance, an implementation that chooses M = 10 and C = 5 would be referred to as Tleilax-10+5.
As for the interconnect between layers, connections are assigned by the following iterative process. A list of N indices, 0 through N-1, is maintained. The connection for node N is chosen from index I of the list, and removed, according to the following equation:
I = (previous_nonce[N] % length(index_list))
Where previous_nonce[N] is the Nth hexadecimal digit of the previous block's nonce. This connection pattern is then duplicated for each layer.
The following is an example of the entire process, except with decimal numbers instead of hexadecimal for easily-understandable arithmetic:
previous_nonce = 122799, M = 6, C = 2
N = (previous_nonce % M) + C = (122799 % 6) + 2 = 5
=> The hashing scheme is 5 x 5
Index List: [0, 1, 2, 3, 4]
I0 = (previous_nonce[N] % length(index_list)) = (9 % 5) = 4
=> Node 0 chooses the 4th index in the list as its connection => 0 connects to 4
Index List: [0, 1, 2, 3]
I1 = (9 % 4) = 1
=> Node 1 chooses the 1st index in the list as its connection => 1 connects to 1
Index List: [0, 2, 3]
I2 = (7 % 3) = 1
=> Node 2 chooses the 1st index in the list as its connection => 2 connects to 2
Index List: [0, 3]
I3 = (2 % 2) = 0
=> Node 3 chooses the 0th index in the list as its connection => 3 connects to 0
=> Node 4 is left with the remaining index => 4 connects to 3
This produces the following hashing architecture:
Finally, as shown in the figure above, all hashing units in the first layer receive the same input, and the outputs of the last layer are all added to produce the output. For this addition, unsigned integer overflow is expected behavior. Additionally, if N exceeds the number of digits of the previous nonce, the process simply wraps around to the first digit once it uses each digit.
Implementations of Tleilax are also free to select any given hash function, although SHA-256 is recommended for its ease of rolling/unrolling. Altogether, the repetitive design of the algorithm is such that it can be scaled up or down to consume as many or as few resources as desired. Individual hashing units can be rolled or unrolled and layers can be physically repeated or just looped. A small FPGA might just implement a single, heavily-rolled hashing unit, with intermediate results being stored by the host in memory. On the other extreme, a large FPGA might implement the hashing architecture fully unrolled, with each layer's interconnect routed in hardware, providing maximum throughput.
ImplementationUnfortunately, I have been unable to develop a complete and stable implementation of Tleilax. During the contest I had an unexpected career change and long-distance relocation, which disrupted my progress on the project. However, I architected an implementation of Tleilax for the Varium C1100 as follows:
On the host, a C++ runtime gets the blockchain transactions and previous block's nonce. It runs the Tleilax algorithms for determining N and the layer interconnect. Based on this, it generates Verilog corresponding to the hashing architecture and the available FPGA resources. This hardware is then synthesized and implemented by Vivado, and programmed to the Varium C1100. The runtime and FPGA communicate over DMA, with the runtime driving mining until a golden nonce is found.
Challenges and Future WorkThe primary challenge for Tleilax is determining how ASIC- or GPU-resistant it truly is. One could imagine an ASIC with an array of hashing units and a performant interconnect. My hope is that the changing dimensions of the hashing architecture would render this suboptimal. One could also further protect against this by perhaps designing a scheme in which hash functions change from block to block. As for GPUs, I believe that for sufficient N the irregularity and complexity of the interconnect prevents efficient Single-Instruction Multiple-Data (SIMD) programming on a GPU. One could also further protect against GPUs by designing a scheme in which the interconnect for each layer is different.
Additionally, there is the consideration that due to the need to synthesize and implement Verilog, Tleilax is actually bounded by the compilation resources of the host. Unfortunately, due to the nature of needing to compile new hardware for reconfiguration, it seems that this is a limitation of any algorithm designed for Proof-of-Configurability. With sufficient block difficulty, this should be mitigated by block mining time greatly exceeding compilation time.
Finally, the most obvious future work is to complete an implementation of the runtime. Manually implementing a given hashing architecture in Verilog for a given set of FPGA resources is straightforward enough, but dynamically scaling down the hashing according to available resources introduces a great deal of complexity. An implementation would also demonstrate whether mining with Tleilax on FPGA might be more energy efficient than traditional Proof-of-Work mining.



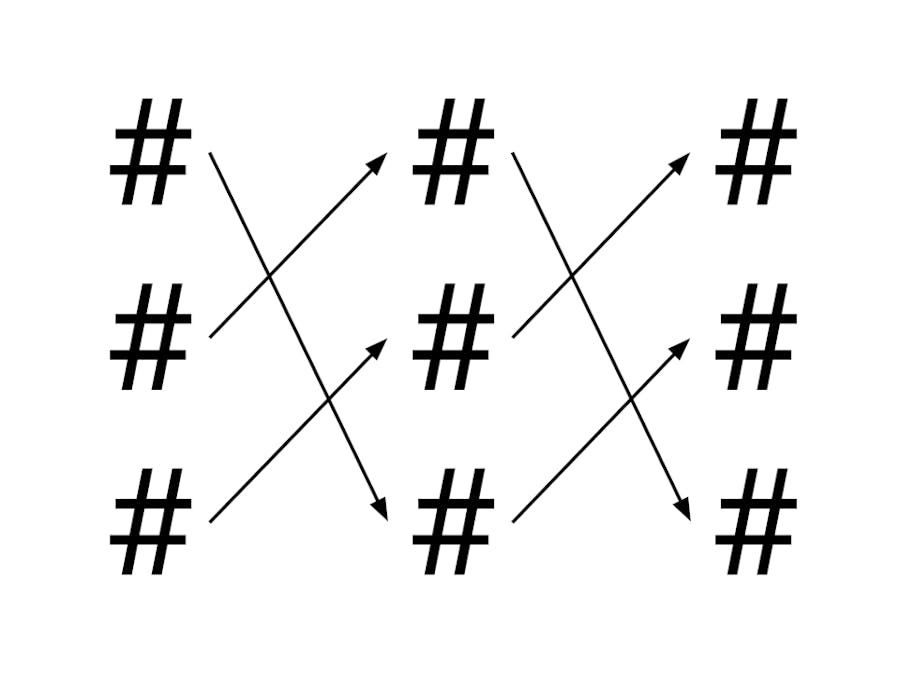





Comments
Please log in or sign up to comment.