Peg Insertion:
Point 1-2: Move the robot in a straight line to a position of your choice from itsresting position.
Point 2-3: Using a number of straight line trajectories, move the robot’s peg just above the hole that is directly to the left of the robot.
Point 3-4: Insert the robot’s peg into the hole so that the peg is inserted two inches. A red line on the peg that indicates the needed depth. The peg must stay in the hole for at least 0.5 seconds so that we can measure if the peg went deep enough into the hole. Then have the robot pull its peg out of the hole.
Obstacle Avoidance:
Point 4-5: Use a number of straight line trajectories to avoid the obstacles in the robot’s path and bring the peg to the entrance of the zig-zag. The entrance is on the robot’s left.
Zig-Zag Maneuver
Point 5-7: Navigate the peg through the zig zag. Here rotate the end effector coordinate frame about Z so that Kp and Kd gains perpendicular to lines through the zig zag can be weakened. There is another red line on the peg that indicates the depth the peg needs to be inside the zig zag. It is around 20 mm or so. The peg must enter the and exit the zig zag. The peg down cannot be brought down into the zig zag nor can be raised the peg before the peg has fully exited the zig zag.
Egg Press:
Point 7-8: After exiting the zig zag, use a number of straight line trajectories tobring the peg just above the egg.
Point 8-9: Once above the egg, push down on the egg with the peg so that the scale reads in the range 500 to 1000 grams. The peg must press down on the egg in that force range for two seconds.
Point 9-10: Once two seconds have elapsed, gently remove force from the egg and then use some straight line trajectories to move the robot arm to its theta1motor = 0, theta2motor=0, theta3motor=0 position, corresponding to (x, y, z)=(10, 0, 20) inches.
Method1. Straight Line TrajectoryAll the above tasks were completed using straight line trajectory.
Where, xd, yd, zd is the function of desired coordinates in x y z axis at time t, xa, ya, za = coordinates of point a (starting point), xb, yb, zb = coordinates of point b (end point), t_start is the starting time stamp, and t_total is the specified time for this entire straight-line trajectory.
There were total of 12 different points defined in task space for our trajectory:
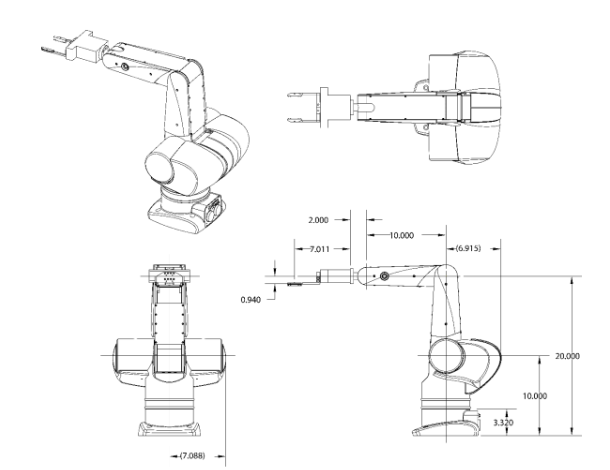
Point 0 (or 14) Home Position : This is a initialization position of the robot as shown below, *Note that this is different from the "start position"
Point 1 : Point above the Hole
Point 2: Inside the Hole
Point 3: Midpoint to the Curve (where this is a point made to avoid colliding with the cardboard obstacle)
Point 4: Curve Entrance
Point 5: First Curve (Going through)
Point 6: Straight Part (of the Curve)
Point 7: Second Curve (Going through)
Point 8: Curve Exit
Point 9: Above Curve Exit
Point 10: Above the Egg
Point 11: Pressing Down on the Egg
*Note that in our code there are 15 total defined waypoints, which includes a repetitive points to either stay or to go back to the previously defined points.
struct Point wp[] = {
{0.254, 0.0, 0.508, 0.0}, // Point 0 (HOME POSITION)
{0.038054874, 0.249578774, 0.22, 1.0}, // Point 1 (Above the Hole)
{0.038054874, 0.249578774, 0.122, 1.0}, // Point 2 (Inside the Hole)
{0.038054874, 0.249578774, 0.122, 0.5}, // Point 2 STAY for 2 seconds
{0.038054874, 0.249578774, 0.22, 1.0}, // Point 3 (Above the Hole)
{0.278772503, 0.104385808, 0.22, 1.0}, // Point 4 (Midpoint to the Curve)
{0.428007482, 0.0979673564, 0.20, 0.75}, // Point 5 (Curve Entrance)
{0.43283993, 0.0715207011, 0.20, 0.2}, // Point 6 (First Curve)
{0.432613403, 0.0393368863, 0.20, 0.5}, // Point 7 (Straight Part)
{0.357446969, 0.0185978226, 0.20, 0.5}, // Point 8 (Second Curve)
{0.421108186, -0.0472436917, 0.20, 0.5}, // Point 9 (Curve Exit)
{0.421108186, -0.0452436917, 0.31, 0.5}, // Point 10 (Above Curve Exit)
{0.270858706, 0.170081974, 0.31, 1.0}, // Point 11 (Above the Egg)
{0.270858706, 0.170081974, 0.273, 3.0}, // Point 12 (Press Down)
{0.270858706, 0.170081974, 0.273, 2.0}, // Point 12 STAY for 2 seconds
{0.270858706, 0.170081974, 0.30, 1.0}, // Point 13 (Above the Egg)
{0.254, 0.0, 0.508, 2.0} // Point 14(0) (HOME POSITION)
};Impedance Controller was used to navigate robot to the desired location.Depending on the waypoint, different PD Values were used to make trajectory smoother and stable.The initial Kp gains (x, y, z) of (960, 600, 720) and Kd gains (x, y, z) of (48, 48, 60) were used. For moving from Home Position to the Initial Position, the Kp gains were scaled down to (560, 350, 420) along with the Kd gains (x, y, z) of (28, 28, 35).
The Impedance Control shined when navigating through the curve, where force of specific axis was weakened to allow free movement. This allowed the robot to navigate through the curve without deriving the actual curved trajectory. Even if precise trajectory derived, any steady state error of the robot position could lead to instability and failure navigating through the curve.
The image of the curved line trajectory in shown below:
The orange solid arrows indicates straight line trajectory from a point to the next desired point.
The yellow dotted arrows is a desired axis to be controlled to allow free movement in that direction. This was set differently in each waypoints.
From the point Curve Entrance to First Curve, the PD gains with theta_z = 0 (original x axis) was set to 0.
From the point First Curve to Second Curve, the PD gains with theta_z = 7*pi/12 (x axis rotated CCW by 105 degrees) was set to 0.
Again from the point Second Curve to Curve Exit, the PD gains with theta_z = 0 (original x axis) was set to 0.
After exiting the curve all the PD gains were reset to the original value of Kp gains (x, y, z) of (960, 600, 720) and Kd gains (x, y, z) of (48, 48, 60).
*Note that the motors will not generate any torque along the weakened axis (yellow dashed arrow), and the contact force from the wall helps the end-effector moves along the zig-zag slot by limiting/allowing movement in corresponding directions.
// Waypoint 6 (Inside the Curve) -> 7 (First Curve)
if (ts[7] <= t && t < ts[8])
{
thetaz = 0;
KPxn = 0;
KDxn = 0;
xd = wp[7].x + dx[8] * (t - ts[7]) / wp[8].dt;
yd = wp[7].y + dy[8] * (t - ts[7]) / wp[8].dt;
zd = wp[7].z + dz[8] * (t - ts[7]) / wp[8].dt;
xd_dot = dx[8] / wp[8].dt;
yd_dot = dy[8] / wp[8].dt;
zd_dot = dz[8] / wp[8].dt;
waypoint = 7;
}
// Waypoint 7 (First Curve) -> 8 (Second Curve)
if (ts[8] <= t && t < ts[9])
{
thetaz = 7 * PI / 12;
KPxn = 0;
KDxn = 0;
xd = wp[8].x + dx[9] * (t - ts[8]) / wp[9].dt;
yd = wp[8].y + dy[9] * (t - ts[8]) / wp[9].dt;
zd = wp[8].z + dz[9] * (t - ts[8]) / wp[9].dt;
xd_dot = dx[9] / wp[9].dt;
yd_dot = dy[9] / wp[9].dt;
zd_dot = dz[9] / wp[9].dt;
waypoint = 8;
}
// Waypoint 8 (Second Curve) -> 9 (Curve Exit)
if (ts[9] <= t && t < ts[10])
{
thetaz = 0;
KPxn = 0;
KDxn = 0;
xd = wp[9].x + dx[10] * (t - ts[9]) / wp[10].dt;
yd = wp[9].y + dy[10] * (t - ts[9]) / wp[10].dt;
zd = wp[9].z + dz[10] * (t - ts[9]) / wp[10].dt;
xd_dot = dx[10] / wp[10].dt;
yd_dot = dy[10] / wp[10].dt;
zd_dot = dz[10] / wp[10].dt;
waypoint = 9;
}
// Waypoint 9 (Curve Exit) -> 10 (Above Curve Exit)
if (ts[10] <= t && t < ts[11])
{
KPxn = 1.2 * 800; // 200
KPyn = 1.2 * 500; // 120
KPzn = 1.2 * 600; // 90
// Derivative Gains Kd
KDxn = 1.2 * 40.0; // 6
KDyn = 1.2 * 40.0; // 5
KDzn = 1.2 * 50.0; // 7
xd = wp[10].x + dx[11] * (t - ts[10]) / wp[11].dt;
yd = wp[10].y + dy[11] * (t - ts[10]) / wp[11].dt;
zd = wp[10].z + dz[11] * (t - ts[10]) / wp[11].dt;
xd_dot = dx[11] / wp[11].dt;
yd_dot = dy[11] / wp[11].dt;
zd_dot = dz[11] / wp[11].dt;
waypoint = 10;Position control of the robot end effector was used to reach the desired force on the scale as the compressive force is directly proportional to the compressed displacement of the spring. The target readings of the scale is within 500g to 1000g.
After several trials, the distance (z axis coordinate) from the ground to the Target Point was set to 0.278 m, which yielded around 680 grams of reading on the scale. Note that the testing with the actual egg was changed to 0.273 m, which yielded around 540 grams of readings.
DEMO:Meet the Team :)+Special Thanks to Professor Yim, Negesh and Negin!
Also, we miss you Dan.
![[UIUC] ME446 - Robot Dynamics and Controls Final Project](https://prod.hackster-cdn.online/assets/transparent-a0c1e3063bcabc548a5f3fa7328f3c1c97f747e6e764da4c14439567baa79ae1.gif)


![[UIUC] ME446 - Robot Dynamics and Controls Final Project](https://hackster.imgix.net/uploads/attachments/1711314/_YzDiYAsfYh.blob?auto=compress%2Cformat&w=900&h=675&fit=min)





Comments
Please log in or sign up to comment.