Hardware components | ||||||
 |
| × | 1 | |||
 |
| × | 1 | |||
 |
| × | 1 | |||
 |
| × | 1 | |||
Software apps and online services | ||||||
 |
| |||||
 |
| |||||
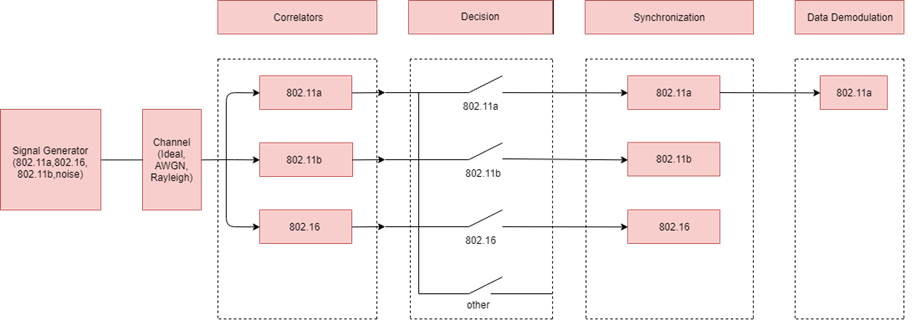
•This project investigates the detection, classification, frame synchronization, and demodulation of wireless networkingwaveforms by a digital receiver.
•To do this, preamble structure is used.
•Three commercial wireless networking standards- IEEE 802.11a, IEEE 802.11b, and IEEE 802.16 are developed
•Firstly, to understand which preamble we used, cross correlation is done
•Secondly, there should be a decision threshold to distinguish between signal and noise, and it is used in signal detection.
•At the end of the project, we’ll reach the ability to signal detection and frame synchronization of multiple wireless networking waveforms.
package Correlation IS
TYPE int_vector is ARRAY(integer RANGE <>) OF integer;
end;
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use work.Correlation.ALL;
entity correlation4 is
port (clk:in std_logic;
C:out int_vector(1 to 5)
);
end correlation4;
architecture Behavioral of correlation4 is
constant zeros:integer:=0;
signal x:int_vector(1 to 4);
signal h:int_vector(1 to 2);
begin
x<=(-1,2,1,-3);
h<=(2,1);
process (clk,x,h)
variable x1:int_vector(1 to 7);
variable sum:integer := 0;
variable corr:integer;
variable a:integer:=5;
variable m:integer range 1 to 2:=1;
variable k:integer range 1 to 5:=1;
begin
x1:=x&zeros&zeros&zeros;
if (rising_edge(clk)) then
corr := h(m)*x1(m+a-1);
sum := sum + corr;
if (m<2) then
m:=m+1;
else
m:=1;
if(a>1) then
a:=a-1;
end if;
C(k) <= sum ;
sum:=0;
k:=k+1;
end if;
end if;
end process;
end Behavioral;
function normC=n_crosscorr(x,y)
L=length(x)+length(y)-1;
a=L;
y1=[zeros(1,length(y)-1),y,zeros(1,length(x)-1)];
corr=0;
C=0;
csum=0;
for k=1:L
for m=1:length(x)
corr=conj(x(m)).*y1(m+a-1);
csum=corr+csum;
end
a=a-1;
C(k)=csum;
csum=0;
end
normC=C./max(C(:));
end
close all;
clear all;
clc;
short_sym=[(0.023+0.023j) (-0.132 +0.002j) (-0.013-0.079j) (0.143-0.013j)...
(0.092+0.000j) (0.143-0.013j) (-0.013-0.079j) (-0.132+0.002j)...
(0.046+0.046j) (0.002-0.132j) (-0.079-0.013j) (-0.013+0.143j)...
(0.000 +0.092j) (-0.013+0.143j) (-0.079-0.013j) (0.002 -0.132j)];%
cp=[(-0.078+0.000j) (0.012-0.098j) (0.092-0.106j) (-0.092-0.115j)...
(-0.003-0.054j) (0.075+0.074j) (-0.127+0.021j) (-0.122+0.017j)...
(-0.035+0.151j) (-0.056+0.022j ) (-0.060-0.081j) (0.070-0.014j)...
(0.082-0.092j) (-0.131-0.065j) (-0.057-0.039j) (0.037-0.098j)...
(0.062+0.062j) (0.119+0.004j) (-0.022-0.161j) (0.059+0.015j)...
(0.024+0.059) (-0.137+0.047j) (0.001+0.115j) (0.053-0.004j)...
(0.098+0.026j) (-0.038+0.106j) (-0.115+0.055j) (0.060+0.088j)...
(0.021-0.028j) (0.097-0.083j) (0.040+0.111j) (-0.005+0.120j) ];
long_sym=[(0.156+0.000j) (-0.005+(-0.120j)) (0.040+(-0.111j)) (0.097+0.083j)...
(0.021+0.028j) (0.060+(-0.088j)) (-0.115+(-0.055j)) (-0.038+(-0.106j))...
(0.098+(-0.026j)) (0.053+0.004j) (0.001-0.115j) (-0.137-0.047j)...
(0.024+(-0.059j)) (0.059-0.015j) (-0.022+0.161j) (0.119-0.004j)...
(0.062+(-0.062j)) (0.037+0.098j) (-0.057+0.039j) (-0.131+0.065j)...
(0.082+0.092j) (0.070+0.014j) (-0.060+0.081j) (-0.056-0.022j)...
(-0.035+(-0.151j)) (-0.122+(-0.017j)) (-0.127+(-0.021j)) (0.075+(-0.074j))...
(-0.003+(0.054j)) (-0.092+0.115j) (0.092+0.106j) (0.012+0.098j)...
(-0.156+0.000j) (0.012+(-0.098j)) (0.092+(-0.106j)) (-0.092+(-0.115j))...
(-0.003+(-0.054j)) (0.075+0.074j) (-0.127+0.021j) (-0.122+0.017j)...
(-0.035+0.151j) (-0.056+0.022j) (-0.060-0.081j) (0.070+(-0.014j))...
(0.082+(-0.092j)) (-0.131+(-0.065j)) (-0.057+(-0.039j)) (0.037+(-0.098j))...
(0.062+0.062j) (0.119+0.004j) (-0.022+(-0.161j)) (0.059+0.015j)...
(0.024+0.059j) (-0.137+0.047j) (0.001+0.115j) (0.053+(-0.004j))...
(0.098+0.026j) (-0.038+0.106j) (-0.115+0.055j) (0.060+0.088j)...
(0.021+(-0.028j)) (0.097+(-0.083j)) (0.040+0.111j) (-0.005+0.120j)];
x=[short_sym short_sym short_sym short_sym short_sym short_sym short_sym short_sym short_sym short_sym cp long_sym long_sym ];
y=[short_sym zeros(1,304)];
z=[long_sym zeros(1,256)];
short_corr=n_crosscorr(x,y);
figure(1);
stem(short_corr);
title('short preamble ');
axis([300 600 0 1])
long_corr=n_crosscorr(x,z);
figure(2);
stem(long_corr);
title ('long preamble');
axis([300 600 0 1])
clear all;close all;clc;
onalti=[0.046+0.046i -0.1324+0.0023i -0.0135-0.0785i 0.1428-0.0127i 0.092 0.1428-0.0127i -0.0135-0.0785i -0.1324+0.0023i...
0.046+0.046i 0.0023-0.1324i -0.0785-0.0135i -0.0127+0.1428i 0.092i -0.0127+0.1428i -0.0785-0.0135i 0.0023-0.1324i];%short
otuziki=[(-0.078+0.000j) (0.012-0.098j) (0.092-0.106j) (-0.092-0.115j)...
(-0.003-0.054j) (0.075+0.074j) (-0.127+0.021j) (-0.122+0.017j)...
(-0.035+0.151j) (-0.056+0.022j ) (-0.060-0.081j) (0.070-0.014j)...
(0.082-0.092j) (-0.131-0.065j) (-0.057-0.039j) (0.037-0.098j)...
(0.062+0.062j) (0.119+0.004j) (-0.022-0.161j) (0.059+0.015j)...
(0.024+0.059) (-0.137+0.047j) (0.001+0.115j) (0.053-0.004j)...
(0.098+0.026j) (-0.038+0.106j) (-0.115+0.055j) (0.060+0.088j)...
(0.021-0.028j) (0.097-0.083j) (0.040+0.111j) (-0.005+0.120j) ];
altmisdort=[(0.156+0.000j) (-0.005+(-0.120j)) (0.040+(-0.111j)) (0.097+0.083j)...
(0.021+0.028j) (0.060+(-0.088j)) (-0.115+(-0.055j)) (-0.038+(-0.106j))...
(0.098+(-0.026j)) (0.053+0.004j) (0.001-0.115j) (-0.137-0.047j)...
(0.024+(-0.059j)) (0.059-0.015j) (-0.022+0.161j) (0.119-0.004j)...
(0.062+(-0.062j)) (0.037+0.098j) (-0.057+0.039j) (-0.131+0.065j)...
(0.082+0.092j) (0.070+0.014j) (-0.060+0.081j) (-0.056-0.022j)...
(-0.035+(-0.151j)) (-0.122+(-0.017j)) (-0.127+(-0.021j)) (0.075+(-0.074j))...
(-0.003+(0.054j)) (-0.092+0.115j) (0.092+0.106j) (0.012+0.098j)...
(-0.156+0.000j) (0.012+(-0.098j)) (0.092+(-0.106j)) (-0.092+(-0.115j))...
(-0.003+(-0.054j)) (0.075+0.074j) (-0.127+0.021j) (-0.122+0.017j)...
(-0.035+0.151j) (-0.056+0.022j) (-0.060-0.081j) (0.070+(-0.014j))...
(0.082+(-0.092j)) (-0.131+(-0.065j)) (-0.057+(-0.039j)) (0.037+(-0.098j))...
(0.062+0.062j) (0.119+0.004j) (-0.022+(-0.161j)) (0.059+0.015j)...
(0.024+0.059j) (-0.137+0.047j) (0.001+0.115j) (0.053+(-0.004j))...
(0.098+0.026j) (-0.038+0.106j) (-0.115+0.055j) (0.060+0.088j)...
(0.021+(-0.028j)) (0.097+(-0.083j)) (0.040+0.111j) (-0.005+0.120j)];
preamble=[onalti onalti onalti onalti onalti onalti onalti onalti onalti onalti otuziki altmisdort altmisdort ];
sample=100;
st=0.11;%0.11
a1=0;
std_signal=std(onalti);
for c=1:48
for t=1:sample
nois = st/(sqrt(2)).*((wgn(1,16,0))+(i*wgn(1,16,0)));
% y1=0;
% x1=0;
% payda1=0;
% payda2=0;
x1=onalti;
y1=nois+onalti;
payda1=0.0413;
payda2=sum((abs(y1)).^2)^2;
% std_signal=std((y1));
a1(t)=abs((y1)*(x1')).^2;
a2(t)=abs((y1)*(y1')).^2;
end
var1(c)=var(a1./payda1);
var2(c)=var(a2./payda2);
k=sum(a1)/payda1;
m=sum(a2)/payda2;
n=sum(var1)/payda1;
p=sum(var2)/payda2;
corrMatlab1(c)=k/sample;
varcorrMatlab1(c)=var(a1)/(sample*payda1);
corrMatlab2(c)=m/sample;
varcorrMatlab2(c)=var(a2)/(sample*payda2);
crossteori(c)=1;
ototeori(c)=(std_signal^4)/(((std_signal^2)+(st^2))^2);
st=st-0.0025;%st=st+0.005 st-0.0001
end
stem(corrMatlab1);
hold on
stem(crossteori);
hold on
stem(corrMatlab2);
hold on
stem(ototeori);
legend('CrossSim','CrossTeori','OtoSim','OtoTeori');
st2=0.030;
hs=0;
nois=st2/sqrt(2).*((wgn(1,320,0))+(i*wgn(1,320,0)));
y2=preamble+nois;
hs=abs(xcorr(onalti,y2))./sqrt(0.0413);
figure(2)
plot(hs);
figure(3)
stem(var1);
set(gca,'yscale','log');
hold on
stem(var2);
set(gca,'yscale','log');
Thanks to Orhan Gazi.














Comments
Please log in or sign up to comment.