Hardware components | ||||||
 |
| × | 1 | |||
Software apps and online services | ||||||
| ||||||
| ||||||
| ||||||
Creating privacy-preserving applications using blockchain technology has been a challenge, limiting the potential of smart contracts in privacy sensitive applications. Some applications, such as those dealing with health information or sensitive proprietary information, are unsuitable for current smart contracts.
Existing solutions to preserve privacy on blockchains can be limiting. These solutions may require a user to perform operations on only a single user’s data or require the computation to be done outside the blockchain. These solutions limit the utility of the public blockchain and the benefits that come with it.
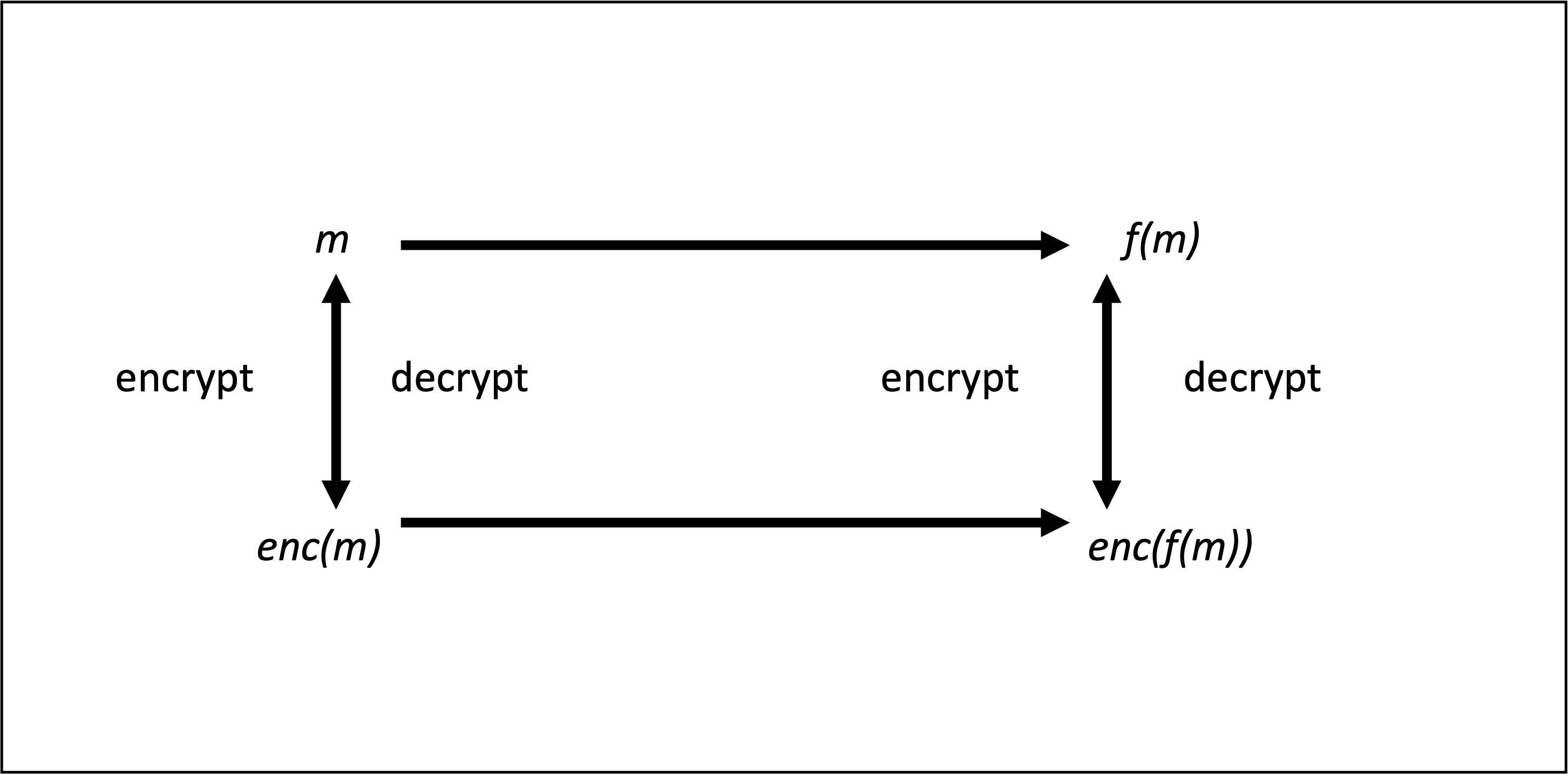
Smart contract using homomorphic encryption can help solve this problem. Homomorphic encryption allows users to perform computations on encrypted data without decrypting the data first. The results of the computation are encrypted. Also, these results, when decrypted, match the results of the same computation performed on the unencrypted data.
By using homomorphic encryption, sensitive data can be used in smart contracts while preserving privacy.
This project uses homomorphic encryption operations in a smart contract. Essentially, the homomorphic encryption operations are included in the smart contract distributed application.
In this project, the homomorphic encryption operations were implemented in a smart contract developed using the Truffle Suite of distributed app tools. This will entail creating a library of functions compatible with the Truffle Suite tools.
As the Truffle Suite uses the Ethereum blockchain, existing hardware for accelerating Ethereum blockchain operations can be used. In this case, the Xilinx C1100 is used.
Smart contracts in the Truffle Suite environment are written in Solidity. Solidity is a statically-typed language, meaning data types like strings, integers, and arrays must be defined. Solidity has a unique type called an address. Addresses are Ethereum addresses, stored as 20 byte values. Every account and smart contract on the Ethereum blockchain has an address and can send and receive Ether to and from this address.
Setting up the Project
This project requires the installation of the following tools.
Node js, available at https://nodejs.org
TruffleSuite, which can be installed by running
npm install -g truffle
once node is installed.
Once TruffleSuite is installed, you can run the init command to create the homomorphic encryption smart contract.
This will create a set of directories to place the smart contract file
contracts/, which contains the Solidity source files for the smart contractmigrations/, which Truffle uses to handle smart contract deploymentstest/, which can contain tests for the smart contractstruffle-config.js, which is the Truffle configuration file
For testing, it is recommended to use Ganache.
Ganache is available at
https://trufflesuite.com/ganache
Ganache allows for simple deployments of private blockchains. This is useful for testing.
Bill of Materials
Aside from computing resources used to develop the smart contract software, the only hardware used was the
pragma solidity >=0.4.20 <0.8.0;
library BigNumber {
/*
* BigNumber is defined as a struct named 'instance' to avoid naming conflicts.
* DO NOT ALLOW INSTANTIATING THIS DIRECTLY - use the '_new' functions defined below.
* Hoping in future Solidity will allow visibility modifiers on structs..
*/
struct instance {
bytes val;
bool neg;
uint bitlen;
}
/** @dev _new: Create a new Bignumber instance.
* overloading allows caller to obtionally pass bitlen where it is known - as it is cheaper to do off-chain and verify on-chain.
* we assert input is in data structure as defined above, and that bitlen, if passed, is correct.
* 'copy' parameter indicates whether or not to copy the contents of val to a new location in memory (for example where you pass the contents of another variable's value in)
* parameter: bytes val - bignum value.
* parameter: bool neg - sign of value
* parameter: uint bitlen - bit length of value
* returns: instance r.
*/
function _new(bytes memory val, bool neg, bool copy) internal view returns(instance memory r){
require(val.length % 32 == 0);
if(!copy) {
r.val = val;
}
else {
// use identity at location 0x4 for cheap memcpy.
// grab contents of val, load starting from memory end, update memory end pointer.
bytes memory val_copy;
assembly{
let size := add(mload(val),0x20)
let new_loc := mload(0x40)
let success := staticcall(450, 0x4, val, size, new_loc, size) // (gas, address, in, insize, out, outsize)
val_copy := new_loc //new bytes value
mstore(0x40, add(new_loc,size)) //update freemem pointer
}
r.val = val_copy;
}
r.neg = neg;
r.bitlen = get_bit_length(val);
}
/** @dev Create a new Bignumber instance.
*
* parameter: bytes val - bignum value
* parameter: bool neg - sign of value
* parameter: uint bitlen - bit length of value
* returns: instance r.
*/
function _new(bytes memory val, bool neg, uint bitlen) internal pure returns(instance memory r){
uint val_msword;
assembly {val_msword := mload(add(val,0x20))} //get msword of result
require((val.length % 32 == 0) && (val_msword>>(bitlen%256)==1));
r.val = val;
r.neg = neg;
r.bitlen = bitlen;
}
/** @dev prepare_add: Initially prepare bignum instances for addition operation; internally calls actual addition/subtraction, depending on inputs.
* In order to do correct addition or subtraction we have to handle the sign.
* This function discovers the sign of the result based on the inputs, and calls the correct operation.
*
* parameter: instance a - first instance
* parameter: instance b - second instance
* returns: instance r - addition of a & b.
*/
function prepare_add(instance memory a, instance memory b) internal pure returns(instance memory r) {
instance memory zero = instance(hex"0000000000000000000000000000000000000000000000000000000000000000",false,0);
if(a.bitlen==0 && b.bitlen==0) return zero;
if(a.bitlen==0) return b;
if(b.bitlen==0) return a;
bytes memory val;
uint bitlen;
int compare = cmp(a,b,false);
if(a.neg || b.neg){
if(a.neg && b.neg){
if(compare>=0) (val, bitlen) = bn_add(a.val,b.val,a.bitlen);
else (val, bitlen) = bn_add(b.val,a.val,b.bitlen);
r.neg = true;
}
else {
if(compare==1){
(val, bitlen) = bn_sub(a.val,b.val);
r.neg = a.neg;
}
else if(compare==-1){
(val, bitlen) = bn_sub(b.val,a.val);
r.neg = !a.neg;
}
else return zero;//one pos and one neg, and same value.
}
}
else{
if(compare>=0){ //a>=b
(val, bitlen) = bn_add(a.val,b.val,a.bitlen);
}
else {
(val, bitlen) = bn_add(b.val,a.val,b.bitlen);
}
r.neg = false;
}
r.val = val;
r.bitlen = bitlen;
}
/** @dev bn_add: takes two instance values and the bitlen of the max value, and adds them.
* This function is private and only callable from prepare_add: therefore the values may be of different sizes,
* in any order of size, and of different signs (handled in prepare_add).
* As values may be of different sizes, inputs are considered starting from the least significant words, working back.
* The function calculates the new bitlen (basically if bitlens are the same for max and min, max_bitlen++) and returns a new instance value.
*
* parameter: bytes max - biggest value (determined from prepare_add)
* parameter: bytes min - smallest value (determined from prepare_add)
* parameter: uint max_bitlen - bit length of max value.
* returns: bytes result - max + min.
* returns: uint - bit length of result.
*/
function bn_add(bytes memory max, bytes memory min, uint max_bitlen) private pure returns (bytes memory, uint) {
bytes memory result;
assembly {
let result_start := msize() // Get the highest available block of memory
let uint_max := sub(0,1) // uint max. achieved using uint underflow: 0xffff...ffff
let carry := 0
let max_ptr := add(max, mload(max))
let min_ptr := add(min, mload(min)) // point to last word of each byte array.
let result_ptr := add(add(result_start,0x20), mload(max)) // set result_ptr end.
for { let i := mload(max) } eq(eq(i,0),0) { i := sub(i, 0x20) } { // for(int i=max_length; i!=0; i-=32)
let max_val := mload(max_ptr) // get next word for 'max'
switch gt(i,sub(mload(max),mload(min))) // if(i>(max_length-min_length)). while 'min' words are still available.
case 1{
let min_val := mload(min_ptr) // get next word for 'min'
mstore(result_ptr, add(add(max_val,min_val),carry)) // result_word = max_word+min_word+carry
switch gt(max_val, sub(uint_max,sub(min_val,carry))) // this switch block finds whether or not to set the carry bit for the next iteration.
case 1 { carry := 1 }
default {
switch and(eq(max_val,uint_max),or(gt(carry,0), gt(min_val,0)))
case 1 { carry := 1 }
default{ carry := 0 }
}
min_ptr := sub(min_ptr,0x20) // point to next 'min' word
}
default{ // else: remainder after 'min' words are complete.
mstore(result_ptr, add(max_val,carry)) // result_word = max_word+carry
switch and( eq(uint_max,max_val), eq(carry,1) ) // this switch block finds whether or not to set the carry bit for the next iteration.
case 1 { carry := 1 }
default { carry := 0 }
}
result_ptr := sub(result_ptr,0x20) // point to next 'result' word
max_ptr := sub(max_ptr,0x20) // point to next 'max' word
}
switch eq(carry,0)
case 1{ result_start := add(result_start,0x20) } // if carry is 0, increment result_start, ie. length word for result is now one word position ahead.
default { mstore(result_ptr, 1) } // else if carry is 1, store 1; overflow has occured, so length word remains in the same position.
result := result_start // point 'result' bytes value to the correct address in memory
mstore(result,add(mload(max),mul(0x20,carry))) // store length of result. we are finished with the byte array.
mstore(0x40, add(result,add(mload(result),0x20))) // Update freemem pointer to point to new end of memory.
}
//we now calculate the result's bit length.
//with addition, if we assume that some a is at least equal to some b, then the resulting bit length will be a's bit length or (a's bit length)+1, depending on carry bit.
//this is cheaper than calling get_bit_length.
uint msword;
assembly {msword := mload(add(result,0x20))} // get most significant word of result
if(msword>>(max_bitlen % 256)==1 || msword==1) ++max_bitlen; // if msword's bit length is 1 greater than max_bitlen, OR overflow occured, new bitlen is max_bitlen+1.
return (result, max_bitlen);
}
/** @dev prepare_sub: Initially prepare bignum instances for addition operation; internally calls actual addition/subtraction, depending on inputs.
* In order to do correct addition or subtraction we have to handle the sign.
* This function discovers the sign of the result based on the inputs, and calls the correct operation.
*
* parameter: instance a - first instance
* parameter: instance b - second instance
* returns: instance r - a-b.
*/
function prepare_sub(instance memory a, instance memory b) internal pure returns(instance memory r) {
instance memory zero = instance(hex"0000000000000000000000000000000000000000000000000000000000000000",false,0);
bytes memory val;
int compare;
uint bitlen;
compare = cmp(a,b,false);
if(a.neg || b.neg) {
if(a.neg && b.neg){
if(compare == 1) {
(val,bitlen) = bn_sub(a.val,b.val);
r.neg = true;
}
else if(compare == -1) {
(val,bitlen) = bn_sub(b.val,a.val);
r.neg = false;
}
else return zero;
}
else {
if(compare >= 0) (val,bitlen) = bn_add(a.val,b.val,a.bitlen);
else (val,bitlen) = bn_add(b.val,a.val,b.bitlen);
r.neg = (a.neg) ? true : false;
}
}
else {
if(compare == 1) {
(val,bitlen) = bn_sub(a.val,b.val);
r.neg = false;
}
else if(compare == -1) {
(val,bitlen) = bn_sub(b.val,a.val);
r.neg = true;
}
else return zero;
}
r.val = val;
r.bitlen = bitlen;
}
/** @dev bn_sub: takes two instance values and subtracts them.
* This function is private and only callable from prepare_add: therefore the values may be of different sizes,
* in any order of size, and of different signs (handled in prepare_add).
* As values may be of different sizes, inputs are considered starting from the least significant words, working back.
* The function calculates the new bitlen (basically if bitlens are the same for max and min, max_bitlen++) and returns a new instance value.
*
* parameter: bytes max - biggest value (determined from prepare_add)
* parameter: bytes min - smallest value (determined from prepare_add)
* parameter: uint max_bitlen - bit length of max value.
* returns: bytes result - max + min.
* returns: uint - bit length of result.
*/
function bn_sub(bytes memory max, bytes memory min) private pure returns (bytes memory, uint) {
bytes memory result;
uint carry = 0;
assembly {
let result_start := msize() // Get the highest available block of memory
let uint_max := sub(0,1) // uint max. achieved using uint underflow: 0xffff...ffff
let max_len := mload(max)
let min_len := mload(min) // load lengths of inputs
let len_diff := sub(max_len,min_len) //get differences in lengths.
let max_ptr := add(max, max_len)
let min_ptr := add(min, min_len) //go to end of arrays
let result_ptr := add(result_start, max_len) //point to least significant result word.
let memory_end := add(result_ptr,0x20) // save memory_end to update free memory pointer at the end.
for { let i := max_len } eq(eq(i,0),0) { i := sub(i, 0x20) } { // for(int i=max_length; i!=0; i-=32)
let max_val := mload(max_ptr) // get next word for 'max'
switch gt(i,len_diff) // if(i>(max_length-min_length)). while 'min' words are still available.
case 1{
let min_val := mload(min_ptr) // get next word for 'min'
mstore(result_ptr, sub(sub(max_val,min_val),carry)) // result_word = (max_word-min_word)-carry
switch or(lt(max_val, add(min_val,carry)),
and(eq(min_val,uint_max), eq(carry,1))) // this switch block finds whether or not to set the carry bit for the next iteration.
case 1 { carry := 1 }
default { carry := 0 }
min_ptr := sub(min_ptr,0x20) // point to next 'result' word
}
default{ // else: remainder after 'min' words are complete.
mstore(result_ptr, sub(max_val,carry)) // result_word = max_word-carry
switch and( eq(max_val,0), eq(carry,1) ) // this switch block finds whether or not to set the carry bit for the next iteration.
case 1 { carry := 1 }
default { carry := 0 }
}
result_ptr := sub(result_ptr,0x20) // point to next 'result' word
max_ptr := sub(max_ptr,0x20) // point to next 'max' word
}
//the following code removes any leading words containing all zeroes in the result.
result_ptr := add(result_ptr,0x20)
for { } eq(mload(result_ptr), 0) { result_ptr := add(result_ptr,0x20) } { //for(result_ptr+=32;; result==0; result_ptr+=32)
result_start := add(result_start, 0x20) // push up the start pointer for the result..
max_len := sub(max_len,0x20) // and subtract a word (32 bytes) from the result length.
}
result := result_start // point 'result' bytes value to the correct address in memory
mstore(result,max_len) // store length of result. we are finished with the byte array.
mstore(0x40, memory_end) // Update freemem pointer.
}
uint new_bitlen = get_bit_length(result); //calculate the result's bit length.
return (result, new_bitlen);
}
/** @dev bn_mul: takes two instances and multiplys them. Order is irrelevant.
* multiplication achieved using modexp precompile:
* (a * b) = (((a + b)**2 - (a - b)**2) / 4
* squaring is done in op_and_square function.
*
* parameter: instance a
* parameter: instance b
* returns: bytes res - a*b.
*/
function bn_mul(instance memory a, instance memory b) internal view returns(instance memory res){
res = op_and_square(a,b,0); // add_and_square = (a+b)^2
//no need to do subtraction part of the equation if a == b; if so, it has no effect on final result.
if(cmp(a,b,true)!=0){
instance memory sub_and_square = op_and_square(a,b,1); // sub_and_square = (a-b)^2
res = prepare_sub(res,sub_and_square); // res = add_and_square - sub_and_square
}
res = right_shift(res, 2); // res = res / 4
}
/** @dev op_and_square: takes two instances, performs operation 'op' on them, and squares the result.
* bn_mul uses the multiplication by squaring method, ie. a*b == ((a+b)^2 - (a-b)^2)/4.
* using modular exponentation precompile for squaring. this requires taking a special modulus value of the form:
* modulus == '1|(0*n)', where n = 2 * bit length of (a 'op' b).
*
* parameter: instance a
* parameter: instance b
* parameter: int op
* returns: bytes res - (a'op'b) ^ 2.
*/
function op_and_square(instance memory a, instance memory b, int op) private view returns(instance memory res){
instance memory two = instance(hex"0000000000000000000000000000000000000000000000000000000000000002",false,2);
uint mod_index = 0;
uint first_word_modulus;
bytes memory _modulus;
res = (op == 0) ? prepare_add(a,b) : prepare_sub(a,b); //op == 0: add, op == 1: sub.
uint res_bitlen = res.bitlen;
assembly { mod_index := mul(res_bitlen,2) }
first_word_modulus = uint(1) << ((mod_index % 256)); //set bit in first modulus word.
//we pass the minimum modulus value which would return JUST the squaring part of the calculation; therefore the value may be many words long.
//This is done by:
// - storing total modulus byte length
// - storing first word of modulus with correct bit set
// - updating the free memory pointer to come after total length.
_modulus = hex"0000000000000000000000000000000000000000000000000000000000000000";
assembly {
mstore(_modulus, mul(add(div(mod_index,256),1),0x20)) //store length of modulus
mstore(add(_modulus,0x20), first_word_modulus) //set first modulus word
mstore(0x40, add(_modulus, add(mload(_modulus),0x20))) //update freemem pointer to be modulus index + length
}
//create modulus instance for modexp function
instance memory modulus;
modulus.val = _modulus;
modulus.neg = false;
modulus.bitlen = mod_index;
res = prepare_modexp(res,two,modulus); // ((a 'op' b) ^ 2 % modulus) == (a 'op' b) ^ 2.
}
/** @dev bn_div: takes three instances (a,b and result), and verifies that a/b == result.
* Verifying a bigint division operation is far cheaper than actually doing the computation.
* As this library is for verification of cryptographic schemes it makes more sense that this function be used in this way.
* (a/b = result) == (a = b * result)
* Integer division only; therefore:
* verify ((b*result) + (a % (b*result))) == a.
* eg. 17/7 == 2:
* verify (7*2) + (17 % (7*2)) == 17.
* the function returns the 'result' param passed on successful validation. returning a bool on successful validation is an option,
* however it makes more sense in the context of the calling contract that it should return the result.
*
* parameter: instance a
* parameter: instance b
* parameter: instance result
* returns: 'result' param.
*/
function bn_div(instance memory a, instance memory b, instance memory result) internal view returns(instance memory){
if(a.neg==true || b.neg==true){ //first handle sign.
if (a.neg==true && b.neg==true) require(result.neg==false);
else require(result.neg==true);
} else require(result.neg==false);
instance memory zero = instance(hex"0000000000000000000000000000000000000000000000000000000000000000",false,0);
require(!(cmp(b,zero,true)==0)); //require denominator to not be zero.
if(cmp(result,zero,true)==0){ //if result is 0:
if(cmp(a,b,true)==-1) return result; // return zero if a<b (numerator < denominator)
else assert(false); // else fail.
}
instance memory fst = bn_mul(b,result); // do multiplication (b * result)
if(cmp(fst,a,true)==0) return result; // check if we already have a (ie. no remainder after division). if so, no mod necessary, and return result.
instance memory one = instance(hex"0000000000000000000000000000000000000000000000000000000000000001",false,1);
instance memory snd = prepare_modexp(a,one,fst); //a mod (b*result)
require(cmp(prepare_add(fst,snd),a,true)==0); // ((b*result) + a % (b*result)) == a
return result;
}
function bn_mod(instance memory a, instance memory mod) internal view returns(instance memory res){
instance memory one = instance(hex"0000000000000000000000000000000000000000000000000000000000000001",false,1);
res = prepare_modexp(a,one,mod);
}
/** @dev prepare_modexp: takes base, exponent, and modulus, internally computes base^exponent % modulus, and creates new instance.
* this function is overloaded: it assumes the exponent is positive. if not, the other method is used, whereby the inverse of the base is also passed.
*
* parameter: instance base
* parameter: instance exponent
* parameter: instance modulus
* returns: instance result.
*/
function prepare_modexp(instance memory base, instance memory exponent, instance memory modulus) internal view returns(instance memory result) {
require(exponent.neg==false); //if exponent is negative, other method with this same name should be used.
bytes memory _result = modexp(base.val,exponent.val,modulus.val);
//get bitlen of result (TODO: optimise. we know bitlen is in the same byte as the modulus bitlen byte)
uint bitlen;
assembly { bitlen := mload(add(_result,0x20))}
bitlen = get_word_length(bitlen) + (((_result.length/32)-1)*256);
result.val = _result;
result.neg = (base.neg==false || base.neg && is_odd(exponent)==0) ? false : true; //TODO review this.
result.bitlen = bitlen;
return result;
}
/** @dev prepare_modexp: takes base, base inverse, exponent, and modulus, asserts inverse(base)==base inverse,
* internally computes base_inverse^exponent % modulus and creates new instance.
* this function is overloaded: it assumes the exponent is negative.
* if not, the other method is used, where the inverse of the base is not passed.
*
* parameter: instance base
* parameter: instance base_inverse
* parameter: instance exponent
* parameter: instance modulus
* returns: instance result.
*/
function prepare_modexp(instance memory base, instance memory base_inverse, instance memory exponent, instance memory modulus) internal view returns(instance memory result) {
// base^-exp = (base^-1)^exp
require(exponent.neg==true);
require(cmp(base_inverse, mod_inverse(base,modulus,base_inverse), true)==0); //assert base_inverse == inverse(base, modulus)
exponent.neg = false; //make e positive
bytes memory _result = modexp(base_inverse.val,exponent.val,modulus.val);
//get bitlen of result (TODO: optimise. we know bitlen is in the same byte as the modulus bitlen byte)
uint bitlen;
assembly { bitlen := mload(add(_result,0x20))}
bitlen = get_word_length(bitlen) + (((_result.length/32)-1)*256);
result.val = _result;
result.neg = (base_inverse.neg==false || base.neg && is_odd(exponent)==0) ? false : true; //TODO review this.
result.bitlen = bitlen;
return result;
}
/** @dev modexp: Takes instance values for base, exp, mod and calls precompile for (_base^_exp)%^mod
* Wrapper for built-in modexp (contract 0x5) as described here - https://github.com/ethereum/EIPs/pull/198
*
* parameter: bytes base
* parameter: bytes base_inverse
* parameter: bytes exponent
* returns: bytes ret.
*/
function modexp(bytes memory _base, bytes memory _exp, bytes memory _mod) private view returns(bytes memory ret) {
assembly {
let bl := mload(_base)
let el := mload(_exp)
let ml := mload(_mod)
let freemem := mload(0x40) // Free memory pointer is always stored at 0x40
mstore(freemem, bl) // arg[0] = base.length @ +0
mstore(add(freemem,32), el) // arg[1] = exp.length @ +32
mstore(add(freemem,64), ml) // arg[2] = mod.length @ +64
// arg[3] = base.bits @ + 96
// Use identity built-in (contract 0x4) as a cheap memcpy
let success := staticcall(450, 0x4, add(_base,32), bl, add(freemem,96), bl)
// arg[4] = exp.bits @ +96+base.length
let size := add(96, bl)
success := staticcall(450, 0x4, add(_exp,32), el, add(freemem,size), el)
// arg[5] = mod.bits @ +96+base.length+exp.length
size := add(size,el)
success := staticcall(450, 0x4, add(_mod,32), ml, add(freemem,size), ml)
switch success case 0 { invalid() } //fail where we haven't enough gas to make the call
// Total size of input = 96+base.length+exp.length+mod.length
size := add(size,ml)
// Invoke contract 0x5, put return value right after mod.length, @ +96
success := staticcall(sub(gas, 1350), 0x5, freemem, size, add(96,freemem), ml)
switch success case 0 { invalid() } //fail where we haven't enough gas to make the call
let length := ml
let length_ptr := add(96,freemem)
///the following code removes any leading words containing all zeroes in the result.
//start_ptr := add(start_ptr,0x20)
for { } eq ( eq(mload(length_ptr), 0), 1) { } {
length_ptr := add(length_ptr, 0x20) //push up the start pointer for the result..
length := sub(length,0x20) //and subtract a word (32 bytes) from the result length.
}
ret := sub(length_ptr,0x20)
mstore(ret, length)
// point to the location of the return value (length, bits)
//assuming mod length is multiple of 32, return value is already in the right format.
//function visibility is changed to internal to reflect this.
//ret := add(64,freemem)
mstore(0x40, add(add(96, freemem),ml)) //deallocate freemem pointer
}
}
/** @dev modmul: Takes instances for a, b, and modulus, and computes (a*b) % modulus
* We call bn_mul for the two input values, before calling modexp, passing exponent as 1.
* Sign is taken care of in sub-functions.
*
* parameter: instance a
* parameter: instance b
* parameter: instance modulus
* returns: instance res.
*/
function modmul(instance memory a, instance memory b, instance memory modulus) internal view returns(instance memory res){
res = bn_mod(bn_mul(a,b),modulus);
}
/** @dev mod_inverse: Takes instances for base, modulus, and result, verifies (base*result)%modulus==1, and returns result.
* Similar to bn_div, it's far cheaper to verify an inverse operation on-chain than it is to calculate it, so we allow the user to pass their own result.
*
* parameter: instance base
* parameter: instance modulus
* parameter: instance user_result
* returns: instance user_result.
*/
function mod_inverse(instance memory base, instance memory modulus, instance memory user_result) internal view returns(instance memory){
require(base.neg==false && modulus.neg==false); //assert positivity of inputs.
/*
* the following proves:
* - user result passed is correct for values base and modulus
* - modular inverse exists for values base and modulus.
* otherwise it fails.
*/
instance memory one = instance(hex"0000000000000000000000000000000000000000000000000000000000000001",false,1);
require(cmp(modmul(base, user_result, modulus),one,true)==0);
return user_result;
}
/** @dev is_odd: returns 1 if instance value is an odd number and 0 otherwise.
*
* parameter: instance _in
* returns: uint ret.
*/
function is_odd(instance memory _in) internal pure returns(uint ret){
assembly{
let in_ptr := add(mload(_in), mload(mload(_in))) //go to least significant word
ret := mod(mload(in_ptr),2) //..and mod it with 2.
}
}
/** @dev cmp: instance comparison. 'signed' parameter indiciates whether to consider the sign of the inputs.
* 'trigger' is used to decide this -
* if both negative, invert the result;
* if both positive (or signed==false), trigger has no effect;
* if differing signs, we return immediately based on input.
* returns -1 on a<b, 0 on a==b, 1 on a>b.
*
* parameter: instance a
* parameter: instance b
* parameter: bool signed
* returns: int.
*/
function cmp(instance memory a, instance memory b, bool signed) internal pure returns(int){
int trigger = 1;
if(signed){
if(a.neg && b.neg) trigger = -1;
else if(a.neg==false && b.neg==true) return 1;
else if(a.neg==true && b.neg==false) return -1;
}
if(a.bitlen>b.bitlen) return 1*trigger;
if(b.bitlen>a.bitlen) return -1*trigger;
uint a_ptr;
uint b_ptr;
uint a_word;
uint b_word;
uint len = a.val.length; //bitlen is same so no need to check length.
assembly{
a_ptr := add(mload(a),0x20)
b_ptr := add(mload(b),0x20)
}
for(uint i=0; i<len;i+=32){
assembly{
a_word := mload(add(a_ptr,i))
b_word := mload(add(b_ptr,i))
}
if(a_word>b_word) return 1*trigger;
if(b_word>a_word) return -1*trigger;
}
return 0; //same value.
}
//*************** begin is_prime functions **********************************
//
//TODO generalize for any size input - currently just works for 850-1300 bit primes
/** @dev is_prime: executes Miller-Rabin Primality Test to see whether input instance is prime or not.
* 'randomness' is expected to be provided
* TODO: 1. add Oraclize randomness generation code template to be added to calling contract.
* 2. generalize for any size input (ie. make constant size randomness array dynamic in some way).
*
* parameter: instance a
* parameter: instance[] randomness
* returns: bool indicating primality.
*/
function is_prime(instance memory a, instance[3] memory randomness) internal view returns (bool){
instance memory zero = instance(hex"0000000000000000000000000000000000000000000000000000000000000000",false,0);
instance memory one = instance(hex"0000000000000000000000000000000000000000000000000000000000000001",false,1);
instance memory two = instance(hex"0000000000000000000000000000000000000000000000000000000000000002",false,2);
if (cmp(a, one, true) != 1){
return false;
} // if value is <= 1
// first look for small factors
if (is_odd(a)==0) {
return (cmp(a, two,true)==0); // if a is even: a is prime if and only if a == 2
}
instance memory a1 = prepare_sub(a,one);
if(cmp(a1,zero,true)==0) return false;
uint k = get_k(a1);
instance memory a1_odd = _new(a1.val, a1.neg, true);
a1_odd = right_shift(a1_odd, k);
int j;
uint num_checks = prime_checks_for_size(a.bitlen);
instance memory check;
for (uint i = 0; i < num_checks; i++) {
check = prepare_add(randomness[i], one);
// now 1 <= check < a.
j = witness(check, a, a1, a1_odd, k);
if(j==-1 || j==1) return false;
}
//if we've got to here, a is likely a prime.
return true;
}
function get_k(instance memory a1) private pure returns (uint k){
k = 0;
uint mask=1;
uint a1_ptr;
uint val;
assembly{
a1_ptr := add(mload(a1),mload(mload(a1))) // get address of least significant portion of a
val := mload(a1_ptr) //load it
}
//loop from least signifcant bits until we hit a set bit. increment k until this point.
for(bool bit_set = ((val & mask) != 0); !bit_set; bit_set = ((val & mask) != 0)){
if(((k+1) % 256) == 0){ //get next word should k reach 256.
a1_ptr -= 32;
assembly {val := mload(a1_ptr)}
mask = 1;
}
mask*=2; // set next bit (left shift)
k++; // increment k
}
}
function prime_checks_for_size(uint bit_size) private pure returns(uint checks){
checks = bit_size >= 1300 ? 2 :
bit_size >= 850 ? 3 :
bit_size >= 650 ? 4 :
bit_size >= 550 ? 5 :
bit_size >= 450 ? 6 :
bit_size >= 400 ? 7 :
bit_size >= 350 ? 8 :
bit_size >= 300 ? 9 :
bit_size >= 250 ? 12 :
bit_size >= 200 ? 15 :
bit_size >= 150 ? 18 :
/* b >= 100 */ 27;
}
function witness(instance memory w, instance memory a, instance memory a1, instance memory a1_odd, uint k) internal view returns (int){
// returns - 0: likely prime, 1: composite number (definite non-prime).
instance memory one = instance(hex"0000000000000000000000000000000000000000000000000000000000000001",false,1);
instance memory two = instance(hex"0000000000000000000000000000000000000000000000000000000000000002",false,2);
w = prepare_modexp(w, a1_odd, a); // w := w^a1_odd mod a
if (cmp(w,one,true)==0) return 0; // probably prime.
if (cmp(w, a1,true)==0) return 0; // w == -1 (mod a), 'a' is probably prime
for (;k != 0; k=k-1) {
w = prepare_modexp(w,two,a); // w := w^2 mod a
if (cmp(w,one,true)==0) return 1; // // 'a' is composite, otherwise a previous 'w' would have been == -1 (mod 'a')
if (cmp(w, a1,true)==0) return 0; // w == -1 (mod a), 'a' is probably prime
}
/*
* If we get here, 'w' is the (a-1)/2-th power of the original 'w', and
* it is neither -1 nor +1 -- so 'a' cannot be prime
*/
return 1;
}
// ******************************** end is_prime functions ************************************
/** @dev right_shift: right shift instance 'dividend' by 'value' bits.
*
* parameter: instance a
* parameter: instance b
* parameter: bool signed
* returns: int.
*/
function right_shift(instance memory dividend, uint value) internal pure returns(instance memory){
//TODO use memcpy for cheap rightshift where input is multiple of 8 (byte size)
bytes memory result;
uint word_shifted;
uint mask_shift = 256-value;
uint mask;
uint result_ptr;
uint max;
uint length = dividend.val.length;
assembly {
max := sub(0,32)
result_ptr := add(mload(dividend), length)
}
for(uint i= length-32; i<max;i-=32){ //for each word:
assembly{
word_shifted := mload(result_ptr) //get next word
switch eq(i,0) //if i==0:
case 1 { mask := 0 } // handles msword: no mask needed.
default { mask := mload(sub(result_ptr,0x20)) } // else get mask.
}
word_shifted >>= value; //right shift current by value
mask <<= mask_shift; // left shift next significant word by mask_shift
assembly{ mstore(result_ptr, or(word_shifted,mask)) } // store OR'd mask and shifted value in-place
result_ptr-=32; // point to next value.
}
assembly{
//the following code removes any leading words containing all zeroes in the result.
result_ptr := add(result_ptr,0x20)
for { } eq(mload(result_ptr), 0) { } {
result_ptr := add(result_ptr, 0x20) //push up the start pointer for the result..
length := sub(length,0x20) //and subtract a word (32 bytes) from the result length.
}
result := sub(result_ptr,0x20)
mstore(result, length)
}
dividend.val = result;
dividend.bitlen = dividend.bitlen-value;
return dividend;
}
function left_shift(instance memory a) internal pure returns(uint) {
//TODO
}
/** @dev hash: sha3 hash a BigNumber instance.
* we hash each instance WITHOUT it's first word - first word is a pointer to the start of the bytes value,
* and so is different for each struct.
*
* parameter: instance a
* returns: bytes32 hash.
*/
function hash(instance memory a) internal pure returns(bytes32 _hash) {
//amount of words to hash = all words of the value and three extra words: neg, bitlen & value length.
assembly {
_hash := keccak256( add(a,0x20), add (mload(mload(a)), 0x60 ) )
}
}
/** @dev get_bit_length: get the bit length of an instance value input.
*
* parameter: bytes a
* returns: uint res.
*/
function get_bit_length(bytes memory val) internal pure returns(uint res){
uint msword;
assembly {msword := mload(add(val,0x20))} //get msword of result
res = get_word_length(msword) + (val.length-32)*8; //get bitlen pf msword, add to size of remaining words.
}
/** @dev get_word_length: get the word length of a uint input - ie. log2_256 (most significant bit of 256 bit value (one EVM word))
* credit: Tjaden Hess @ ethereum.stackexchange
*
* parameter: uint x
* returns: uint y.
*/
function get_word_length(uint x) internal pure returns (uint y){
uint arg = x;
assembly {
x := sub(x,1)
x := or(x, div(x, 0x02))
x := or(x, div(x, 0x04))
x := or(x, div(x, 0x10))
x := or(x, div(x, 0x100))
x := or(x, div(x, 0x10000))
x := or(x, div(x, 0x100000000))
x := or(x, div(x, 0x10000000000000000))
x := or(x, div(x, 0x100000000000000000000000000000000))
x := add(x, 1)
let m := mload(0x40)
mstore(m, 0xf8f9cbfae6cc78fbefe7cdc3a1793dfcf4f0e8bbd8cec470b6a28a7a5a3e1efd)
mstore(add(m,0x20), 0xf5ecf1b3e9debc68e1d9cfabc5997135bfb7a7a3938b7b606b5b4b3f2f1f0ffe)
mstore(add(m,0x40), 0xf6e4ed9ff2d6b458eadcdf97bd91692de2d4da8fd2d0ac50c6ae9a8272523616)
mstore(add(m,0x60), 0xc8c0b887b0a8a4489c948c7f847c6125746c645c544c444038302820181008ff)
mstore(add(m,0x80), 0xf7cae577eec2a03cf3bad76fb589591debb2dd67e0aa9834bea6925f6a4a2e0e)
mstore(add(m,0xa0), 0xe39ed557db96902cd38ed14fad815115c786af479b7e83247363534337271707)
mstore(add(m,0xc0), 0xc976c13bb96e881cb166a933a55e490d9d56952b8d4e801485467d2362422606)
mstore(add(m,0xe0), 0x753a6d1b65325d0c552a4d1345224105391a310b29122104190a110309020100)
mstore(0x40, add(m, 0x100))
let magic := 0x818283848586878898a8b8c8d8e8f929395969799a9b9d9e9faaeb6bedeeff
let shift := 0x100000000000000000000000000000000000000000000000000000000000000
let a := div(mul(x, magic), shift)
y := div(mload(add(m,sub(255,a))), shift)
y := add(y, mul(256, gt(arg, 0x8000000000000000000000000000000000000000000000000000000000000000)))
}
if(arg & arg-1 == 0 && x!=0) ++y; //where x is a power of two, result needs to be incremented. we use the power of two trick here
}
}
pragma solidity >=0.4.22 <0.8.0;
contract Prng {
function Arcfour() public restricted {
this.i = 0;
this.j = 0;
this.S = new Array();
}
// Initialize arcfour context from key, an array of ints, each from [0..255]
function ARC4init(uint key) public restricted {
// var i, j, t;
uint i;
uint j;
uint t;
for(i = 0; i < 256; ++i)
this.S[i] = i;
j = 0;
for(i = 0; i < 256; ++i) {
j = (j + this.S[i] + key[i % key.length]) & 255;
t = this.S[i];
this.S[i] = this.S[j];
this.S[j] = t;
}
this.i = 0;
this.j = 0;
}
function ARC4next() public restricted {
uint t;
this.i = (this.i + 1) & 255;
this.j = (this.j + this.S[this.i]) & 255;
t = this.S[this.i];
this.S[this.i] = this.S[this.j];
this.S[this.j] = t;
return this.S[(t + this.S[this.i]) & 255];
}
Arcfour.prototype.init = ARC4init;
Arcfour.prototype.next = ARC4next;
function prng_newstate() public restricted {
return new Arcfour();
}
// Pool size must be a multiple of 4 and greater than 32.
// An array of bytes the size of the pool will be passed to init()
uint rng_psize = 4;
}
pragma solidity ^0.5.0;
contract HE {
uint bits;
uint n;
uint n2;
uint np1;
uint lambda;
uint pubkey;
uint x;
function lcm(uint a, uint b) public restricted {
return a.divide(a.gcd(b)).multiply(b);
}
function publicKey(uint bits, uint n) public restricted {
this.bits = bits;
this.n = n;
this.n2 = n.square();
this.np1 = n.add(BigInteger.ONE);
//this.rncache = [];
}
function privateKey(uint lambda, uint pubkey) public restricted {
this.lambda = lambda;
this.pubkey = pubkey;
this.x = pubkey.np1.modPow(this.lambda, pubkey.n2).subtract(BigInteger.ONE).divide(pubkey.n).modInverse(pubkey.n);
}
function generateKeys(uint modulusbits) public restricted {
uint p;
uint q;
uint n;
keys = {};
rng = new SecureRandom();
do {
do {
p = new BigInteger(modulusbits >> 1, 1, rng);
} while (!p.isProbablePrime(10));
do {
q = new BigInteger(modulusbits >> 1, 1, rng);
} while (!q.isProbablePrime(10));
n = p.multiply(q);
} while (!(n.testBit(modulusbits - 1)) || (p.compareTo(q) === 0));
keys.pub = new paillier.publicKey(modulusbits, n);
lambda = lcm(p.subtract(BigInteger.ONE), q.subtract(BigInteger.ONE));
keys.sec = new paillier.privateKey(lambda, keys.pub);
return keys;
}
function encrypt(uint m, uint r) public restricted {
if (r) {
var rn = r.modPow(this.n, this.n2);
return (rn.multiply(this.n.multiply(m).add(BigInteger.ONE).mod(this.n2))).mod(this.n2);
} else {
return this.randomize(this.n.multiply(m).add(BigInteger.ONE).mod(this.n2));
}
}
function add(uint a, uint b) public restricted {
return a.multiply(b).remainder(this.n2);
}
function mult(uint a, uint b) public restricted {
return a.modPow(b, this.n2);
}
function randomize(uint a,) public restricted {
uint rn;
if (this.rncache.length > 0) {
rn = this.rncache.pop();
} else {
rn = this.getRN();
}
return (a.multiply(rn)).mod(this.n2);
}
function convertToBn(uint m,) public restricted {
if (typeof(m) == 'string'){
m = new BigInteger(m);
} else if (m.constructor != BigInteger) {
m = new BigInteger(parseInt(m).toString());
}
return m;
}
function getRN() public restricted {
uint r;
rng = new SecureRandom();
do {
r = new BigInteger(this.bits, rng);
// make sure r <= n
} while (r.compareTo(this.n) >= 0);
return r.modPow(this.n, this.n2);
}
function getR() public restricted {
uint r;
rng = new SecureRandom();
do {
r = new BigInteger(this.bits, rng);
// make sure r <= n
} while (r.compareTo(this.n) >= 0);
return r;
}
function precompute(uint n) public restricted {
for (var i = 0; i < n; i++) {
this.rncache.push(this.getRN());
}
}
}



Comments
Please log in or sign up to comment.