The humble FIR filter is one of the most basic building blocks in digital signal processing on an FPGA, so it's important to know how to throw together a basic module of one with a given number of taps and their corresponding coefficient values. Thus, in this mini-series on the practical way of getting started with DSP basics on FPGAs, I'm going to start with a simple 15-tap low pass filter FIR that I generate the initial coefficient values for in Matlab then convert those values for use in a Verilog module.
A finite impulse response or FIR filter is defined as a filter with an impulse response that settles to a zero value over a certain period of time, thus making it finite. This amount of time that it takes the impulse response to settle to zero is directly related to the order of the filter (the number of taps) which is the order of the FIR's underlying transfer function polynomial. A FIR's transfer function contains no feedback, so if you feed in a single impulse of value 1 followed by a bunch of zero values, the output will simply be the coefficient values of the filter.
The role of any filter is for signal conditioning, mainly focusing on the selection of which frequencies to either filter out or allow to pass through. One of the simplest examples of this is the low pass filter, which allows frequencies below a certain threshold (cutoff frequency) to pass while greatly attenuating frequencies above that threshold, as depicted in the figure below.
The main focus of this project is on the implementation of a FIR in HDL (Verilog specifically, but the concept can be easily translated to VHDL), which can be broken down into three main logic components: a circular buffer to clock each sample into that properly accounts for the delays of the serial input, multipliers for each of the taps' coefficient value, and the accumulator register for the summing result from each tap's output.
Since I'm focusing on the mechanics of the FIR in FPGA logic, I just used the FDA Tool in Simulink with Matlab to plug in some simple parameters for a low pass filter and then used the generated coefficient values to calculate into my proper register values for my Verilog module (done in a later step).
I chose to implement a simple 15-tap low pass filter FIR sampling at 1Ms/s with a passband frequency of 200 kHz and a stop band frequency of 355kHz which gave me the following coefficients:
-0.0265
0
0.0441
0
-0.0934
0
0.3139
0.5000
0.3139
0
-0.0934
0
0.0441
0
-0.0265Starting from scratch in a new Vivado project, create a new design source for the FIR module using the Add Sources option in the Flow Navigator window.
Now after deciding on the order (number of taps) for your FIR and obtaining your coefficient values, the next set of parameters that must be defined is the bit width of the input samples, output samples, and the coefficients themselves.
For this FIR, I chose to set my input sample and coefficient registers to be 16 bits wide and my output sample register to be 32 bits since the product of two 16-bit values is a 32-bit value (the widths of the two values being multiplied add to give the width of the product, so if I had chosen 16-bit input samples with 8-bit taps then the output samples would be 24 bits wide).
These values are also all signed, thus the MSB is used as the sign bit and the lower remaining bits are what the value must fit into (be sure to keep this in mind when selecting the initial widths of the input sample register). To set these values as signed data type in Verilog, the keyword signed is used:
reg signed [15:0] register_name;The next thing to address is how to handle the coefficient values in Verilog, the decimal point values need to be converted to fixed point values. Since all of the coefficient values are less than one, all 15 bits (the MSB of the total 16 bits is the signed bit) of my registers can be dedicated to fractional bits. Usually, you have to decide how many bits in the register you want to dedicate to the integer part of the number vs the fractional part of the number. Therefore the math to convert the fractional value taps is:(fractional coefficient value)*(2^(15))Where any decimal value of this product is rounded off and the two's compliment of the value is calculated if the coefficient is negative:
tap0 = twos(-0.0265 * 32768) = 0xFC9C
tap1 = 0
tap2 = 0.0441 * 32768 = 1445.0688 = 1445 = 0x05A5
tap3 = 0
tap4 = twos(-0.0934 * 32768) = 0xF40C
tap5 = 0
tap6 = 0.3139 * 32768 = 10285.8752 = 10285 = 0x282D
tap7 = 0.5000 * 32768 = 16384 = 0x4000
tap8 = 0.3139 * 32768 = 10285.8752 = 10285 = 0x282D
tap9 = 0
tap10 = twos(-0.0934 * 32768) = 0xF40C
tap11 = 0
tap12 = 0.0441 * 32768 = 1445.0688 = 1445 = 0x05A5
tap13 = 0
tap14 = twos(-0.0265 * 32768) = 0xFC9CNow we're finally ready to focus on the logic of the FIR module, the first of which is the circular buffer which brings in a serial input sample stream and creates an array of 15 input samples for the 15 taps of the filter.
always @ (posedge clk)
begin
if(enable_buff == 1'b1)
begin
buff0 <= in_sample;
buff1 <= buff0;
buff2 <= buff1;
buff3 <= buff2;
buff4 <= buff3;
buff5 <= buff4;
buff6 <= buff5;
buff7 <= buff6;
buff8 <= buff7;
buff9 <= buff8;
buff10 <= buff9;
buff11 <= buff10;
buff12 <= buff11;
buff13 <= buff12;
buff14 <= buff13;
end
endNext, the multiply stage multiplies each sample by each of the coefficient values:
/* Multiply stage of FIR */
always @ (posedge clk)
begin
if (enable_fir == 1'b1)
begin
acc0 <= tap0 * buff0;
acc1 <= tap1 * buff1;
acc2 <= tap2 * buff2;
acc3 <= tap3 * buff3;
acc4 <= tap4 * buff4;
acc5 <= tap5 * buff5;
acc6 <= tap6 * buff6;
acc7 <= tap7 * buff7;
acc8 <= tap8 * buff8;
acc9 <= tap9 * buff9;
acc10 <= tap10 * buff10;
acc11 <= tap11 * buff11;
acc12 <= tap12 * buff12;
acc13 <= tap13 * buff13;
acc14 <= tap14 * buff14;
end
end The resulting values from the multiply stage are accumulated by addition in a register which ultimately is the output data stream from the filter.
/* Accumulate stage of FIR */
always @ (posedge clk)
begin
if (enable_fir == 1'b1)
begin
m_axis_fir_tdata <= acc0 + acc1 + acc2 + acc3 + acc4 + acc5 + acc6 + acc7 + acc8 + acc9 + acc10 + acc11 + acc12 + acc13 + acc14;
end
end Finally, the last part of the logic is the interface to stream data to and from the FIR module. The AXI Stream interface is one of the most common, thus what I chose to implement. The key aspects are the valid and ready signals which allow for the control of the flow of data between upstream and downstream devices. This means the FIR module needs to provide a valid signal to its downstream device to indicate that it's output is valid data, as well as be able to pause (but still retain) its output if the downstream device de-asserts its ready signal. The FIR module must also be able to behave this same way with its upstream device on its master side interface.
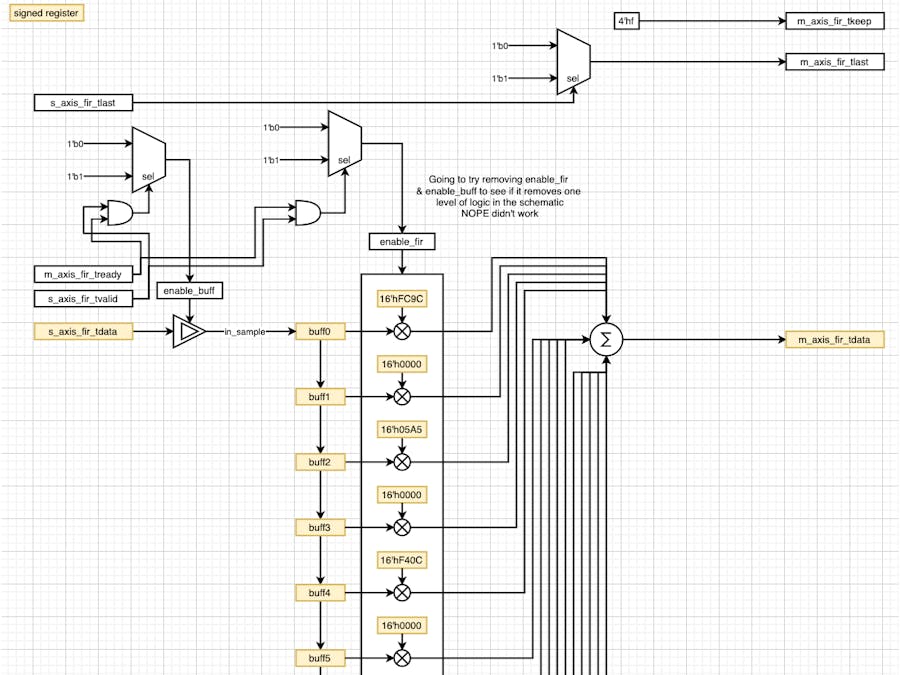
Here's an overview of the logic design for the FIR module:
Notice how the valid and ready signals set the enable value for the input circular buffer and the multiply stage of the FIR and each of the registers that the data or coefficients pass through are declared as signed.
FIR module Verilog code:
`timescale 1ns / 1ps
module FIR(
input clk,
input reset,
input signed [15:0] s_axis_fir_tdata,
input [3:0] s_axis_fir_tkeep,
input s_axis_fir_tlast,
input s_axis_fir_tvalid,
input m_axis_fir_tready,
output reg m_axis_fir_tvalid,
output reg s_axis_fir_tready,
output reg m_axis_fir_tlast,
output reg [3:0] m_axis_fir_tkeep,
output reg signed [31:0] m_axis_fir_tdata
);
always @ (posedge clk)
begin
m_axis_fir_tkeep <= 4'hf;
end
always @ (posedge clk)
begin
if (s_axis_fir_tlast == 1'b1)
begin
m_axis_fir_tlast <= 1'b1;
end
else
begin
m_axis_fir_tlast <= 1'b0;
end
end
// 15-tap FIR
reg enable_fir, enable_buff;
reg [3:0] buff_cnt;
reg signed [15:0] in_sample;
reg signed [15:0] buff0, buff1, buff2, buff3, buff4, buff5, buff6, buff7, buff8, buff9, buff10, buff11, buff12, buff13, buff14;
wire signed [15:0] tap0, tap1, tap2, tap3, tap4, tap5, tap6, tap7, tap8, tap9, tap10, tap11, tap12, tap13, tap14;
reg signed [31:0] acc0, acc1, acc2, acc3, acc4, acc5, acc6, acc7, acc8, acc9, acc10, acc11, acc12, acc13, acc14;
/* Taps for LPF running @ 1MSps with a cutoff freq of 400kHz*/
assign tap0 = 16'hFC9C; // twos(-0.0265 * 32768) = 0xFC9C
assign tap1 = 16'h0000; // 0
assign tap2 = 16'h05A5; // 0.0441 * 32768 = 1445.0688 = 1445 = 0x05A5
assign tap3 = 16'h0000; // 0
assign tap4 = 16'hF40C; // twos(-0.0934 * 32768) = 0xF40C
assign tap5 = 16'h0000; // 0
assign tap6 = 16'h282D; // 0.3139 * 32768 = 10285.8752 = 10285 = 0x282D
assign tap7 = 16'h4000; // 0.5000 * 32768 = 16384 = 0x4000
assign tap8 = 16'h282D; // 0.3139 * 32768 = 10285.8752 = 10285 = 0x282D
assign tap9 = 16'h0000; // 0
assign tap10 = 16'hF40C; // twos(-0.0934 * 32768) = 0xF40C
assign tap11 = 16'h0000; // 0
assign tap12 = 16'h05A5; // 0.0441 * 32768 = 1445.0688 = 1445 = 0x05A5
assign tap13 = 16'h0000; // 0
assign tap14 = 16'hFC9C; // twos(-0.0265 * 32768) = 0xFC9C
/* This loop sets the tvalid flag on the output of the FIR high once
* the circular buffer has been filled with input samples for the
* first time after a reset condition. */
always @ (posedge clk or negedge reset)
begin
if (reset == 1'b0) //if (reset == 1'b0 || tvalid_in == 1'b0)
begin
buff_cnt <= 4'd0;
enable_fir <= 1'b0;
in_sample <= 8'd0;
end
else if (m_axis_fir_tready == 1'b0 || s_axis_fir_tvalid == 1'b0)
begin
enable_fir <= 1'b0;
buff_cnt <= 4'd15;
in_sample <= in_sample;
end
else if (buff_cnt == 4'd15)
begin
buff_cnt <= 4'd0;
enable_fir <= 1'b1;
in_sample <= s_axis_fir_tdata;
end
else
begin
buff_cnt <= buff_cnt + 1;
in_sample <= s_axis_fir_tdata;
end
end
always @ (posedge clk)
begin
if(reset == 1'b0 || m_axis_fir_tready == 1'b0 || s_axis_fir_tvalid == 1'b0)
begin
s_axis_fir_tready <= 1'b0;
m_axis_fir_tvalid <= 1'b0;
enable_buff <= 1'b0;
end
else
begin
s_axis_fir_tready <= 1'b1;
m_axis_fir_tvalid <= 1'b1;
enable_buff <= 1'b1;
end
end
/* Circular buffer bring in a serial input sample stream that
* creates an array of 15 input samples for the 15 taps of the filter. */
always @ (posedge clk)
begin
if(enable_buff == 1'b1)
begin
buff0 <= in_sample;
buff1 <= buff0;
buff2 <= buff1;
buff3 <= buff2;
buff4 <= buff3;
buff5 <= buff4;
buff6 <= buff5;
buff7 <= buff6;
buff8 <= buff7;
buff9 <= buff8;
buff10 <= buff9;
buff11 <= buff10;
buff12 <= buff11;
buff13 <= buff12;
buff14 <= buff13;
end
else
begin
buff0 <= buff0;
buff1 <= buff1;
buff2 <= buff2;
buff3 <= buff3;
buff4 <= buff4;
buff5 <= buff5;
buff6 <= buff6;
buff7 <= buff7;
buff8 <= buff8;
buff9 <= buff9;
buff10 <= buff10;
buff11 <= buff11;
buff12 <= buff12;
buff13 <= buff13;
buff14 <= buff14;
end
end
/* Multiply stage of FIR */
always @ (posedge clk)
begin
if (enable_fir == 1'b1)
begin
acc0 <= tap0 * buff0;
acc1 <= tap1 * buff1;
acc2 <= tap2 * buff2;
acc3 <= tap3 * buff3;
acc4 <= tap4 * buff4;
acc5 <= tap5 * buff5;
acc6 <= tap6 * buff6;
acc7 <= tap7 * buff7;
acc8 <= tap8 * buff8;
acc9 <= tap9 * buff9;
acc10 <= tap10 * buff10;
acc11 <= tap11 * buff11;
acc12 <= tap12 * buff12;
acc13 <= tap13 * buff13;
acc14 <= tap14 * buff14;
end
end
/* Accumulate stage of FIR */
always @ (posedge clk)
begin
if (enable_fir == 1'b1)
begin
m_axis_fir_tdata <= acc0 + acc1 + acc2 + acc3 + acc4 + acc5 + acc6 + acc7 + acc8 + acc9 + acc10 + acc11 + acc12 + acc13 + acc14;
end
end
endmoduleTo test the FIR module, a testbench needs to be created as a new simulation source:
There are two main things that need to be tested in the FIR module: the filter math and the AXI stream interface. To accomplish this, I created a state machine in the test bench that generates a simple 200kHz sine wave and also toggles the valid signal on the slave side and the ready signal on the master side of the FIR's interface.
Testbench for FIR module:
`timescale 1ns / 1ps
module tb_FIR;
reg clk, reset, s_axis_fir_tvalid, m_axis_fir_tready;
reg signed [15:0] s_axis_fir_tdata;
wire m_axis_fir_tvalid;
wire [3:0] m_axis_fir_tkeep;
wire [31:0] m_axis_fir_tdata;
/*
* 100Mhz (10ns) clock
*/
always begin
clk = 1; #5;
clk = 0; #5;
end
always begin
reset = 1; #20;
reset = 0; #50;
reset = 1; #1000000;
end
always begin
s_axis_fir_tvalid = 0; #100;
s_axis_fir_tvalid = 1; #1000;
s_axis_fir_tvalid = 0; #50;
s_axis_fir_tvalid = 1; #998920;
end
always begin
m_axis_fir_tready = 1; #1500;
m_axis_fir_tready = 0; #100;
m_axis_fir_tready = 1; #998400;
end
/* Instantiate FIR module to test. */
FIR FIR_i(
.clk(clk),
.reset(reset),
.s_axis_fir_tdata(s_axis_fir_tdata),
.s_axis_fir_tkeep(s_axis_fir_tkeep),
.s_axis_fir_tlast(s_axis_fir_tlast),
.s_axis_fir_tvalid(s_axis_fir_tvalid),
.m_axis_fir_tready(m_axis_fir_tready),
.m_axis_fir_tvalid(m_axis_fir_tvalid),
.s_axis_fir_tready(s_axis_fir_tready),
.m_axis_fir_tlast(m_axis_fir_tlast),
.m_axis_fir_tkeep(m_axis_fir_tkeep),
.m_axis_fir_tdata(m_axis_fir_tdata));
reg [4:0] state_reg;
reg [3:0] cntr;
parameter wvfm_period = 4'd4;
parameter init = 5'd0;
parameter sendSample0 = 5'd1;
parameter sendSample1 = 5'd2;
parameter sendSample2 = 5'd3;
parameter sendSample3 = 5'd4;
parameter sendSample4 = 5'd5;
parameter sendSample5 = 5'd6;
parameter sendSample6 = 5'd7;
parameter sendSample7 = 5'd8;
/* This state machine generates a 200kHz sinusoid. */
always @ (posedge clk or posedge reset)
begin
if (reset == 1'b0)
begin
cntr <= 4'd0;
s_axis_fir_tdata <= 16'd0;
state_reg <= init;
end
else
begin
case (state_reg)
init : //0
begin
cntr <= 4'd0;
s_axis_fir_tdata <= 16'h0000;
state_reg <= sendSample0;
end
sendSample0 : //1
begin
s_axis_fir_tdata <= 16'h0000;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample1;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample0;
end
end
sendSample1 : //2
begin
s_axis_fir_tdata <= 16'h5A7E;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample2;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample1;
end
end
sendSample2 : //3
begin
s_axis_fir_tdata <= 16'h7FFF;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample3;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample2;
end
end
sendSample3 : //4
begin
s_axis_fir_tdata <= 16'h5A7E;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample4;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample3;
end
end
sendSample4 : //5
begin
s_axis_fir_tdata <= 16'h0000;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample5;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample4;
end
end
sendSample5 : //6
begin
s_axis_fir_tdata <= 16'hA582;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample6;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample5;
end
end
sendSample6 : //6
begin
s_axis_fir_tdata <= 16'h8000;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample7;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample6;
end
end
sendSample7 : //6
begin
s_axis_fir_tdata <= 16'hA582;
if (cntr == wvfm_period)
begin
cntr <= 4'd0;
state_reg <= sendSample0;
end
else
begin
cntr <= cntr + 1;
state_reg <= sendSample7;
end
end
endcase
end
end
endmoduleUnder the simulation sources in the Sources window, set the testbench module as the top level file by right-clicking on it and selecting Set as Top.
With the FIR module and its testbench in place, launch the Simulator in Vivado from the Flow Navigator window, selecting the Run Behavioral Simulation option (which is the only available option if there are no synthesis or implementation results available).
As the behavioral simulation shows, the FIR is filtering the signal properly as well as responding to the AXI stream signals properly.
As many of you will probably notice, running synthesis and implementation on a design using this particular FIR module will result in a design that does not meet timing (I'm sure you seasoned FPGA engineers reading this could already tell that just from looking at the Verilog for the FIR module). This will be addressed in the next installment of this DSP for FPGA series as it offers good insight into how to rethink your design when you can't meeting set-up timing requirements.













Comments